set.seed(2023)
n<-10^4 #Tamañodelamuestra
U<-runif(n)6 Procesos de Montecarlo
6.1 Métodos de MonteCarlo
El método de MonteCarlo es un método numérico usuado para aproximar expresiones matemáticas de un alto grado de complejidad y díficiles de evaluar con exactitud. Los métodos de Montecarlo abarcan una colección de técnicas que permiten obtener soluciones de problemas matemáticos o físicos por medio de pruebas aleatorias repetidas.
Su desarrollo sistemático y su nombre se originó en la década de los 40 del siglo pasado, en referencia al Casino de Montecarlo en Mónaco, usado en el proyecto Manthattan de la bomba atómica y ha mejorado con el pasar del tiempo, gracias a desarrollo de la computación.
6.1.1 Integración de Montecarlo
Para el cálculo de algortimo que usan el Método de Montecarlo, iniciaremos con la estimación de integrales. Estas se basan en dos hechos conocidos:
- Sea \(X\) una variable aleatoria con función de densidad \(\pi(x)\) entonces:
\[E[g(X)]=\int g(x)\pi(x)dx\]
- \(P \left( \displaystyle\lim_{n \rightarrow \infty}\frac{x_1+x_2+...+x_n}{n}=\mu \right)=1\)
En particular tenemos que:
\[\frac{g(x_1)+g(x_2)+...+g(x_n)}{n} \rightarrow E[g(X)]=\theta, \;n \rightarrow \infty\]
Estádistico \(T(X)=\frac{1}{n}\sum g(x_i)\)
Dada una muestra aleatoria simple \(x_1,x_2,...,x_n\) y el estadístico \(T(X)=\frac{1}{n}\sum_{i=1}^n g(x_i)\)
Esperanza del Estadístico
\[E[T(X)]=E[\frac{1}{n}\sum_{i=1}^n g(x_i)]=E[g(X)]\]
Varianza del Estadístico
\[var[T(X)]=Var[\frac{1}{n}\sum_{i=1}^n g(x_i)]=\frac{1}{n}Var(g(X))=\sigma_{g(x)}^2\]
El error al usar el método de Montecarlo es aproximadamente:
\[\frac{\sigma_{g(x)}^2}{\sqrt n}\]
Un intervalo de confianza de nivel \(1-\alpha\) es
\[\left[T(x)\pm z_{\alpha/2}\frac{\sigma_{g(x)}^2}{\sqrt n} \right]\]
6.1.2 Ejemplo 1
Tomemos la función \(g(x)=4\sqrt{1-x^2}\) en el intervalo \([0,1]\), si calculamos la integral:
\(\displaystyle \int_{0}^{1}4\sqrt{1-x^2}dx=\pi\)
Definamos \(X \sim U[0,1]\) lo que implica que \(\pi(X)=1\)
\[\int_{0}^{1}g(x)dx=\int_{0}^{1}g(x)dx=\int_{0}^{1}g(x)\pi(x)dx=E_{U[0,1]}[g(x)]\]
Dado una m.a.s \(u_1,u_2,..., u_3\) de \(U[0,1]\) entonces:
\[\displaystyle\lim_{n \rightarrow \infty}\frac{1}{n}\sum_{i=1}^n g(u_i)=\pi\]
Por lo que podemos aproximar \(\pi\)
\[\frac{1}{n}\sum_{i=1}^n g(u_i)\approx \pi\]
Tomaremos una muestra de \(10^4\) variables aleatorias
construyamos la función \(g(x)\)
g<-Vectorize(function(x) 4*sqrt(1-x^2))Grafiquemos \(g(x)\)
curve(g,0,1,col="blue",lwd=1,main="Grafico de g(X)")
grid()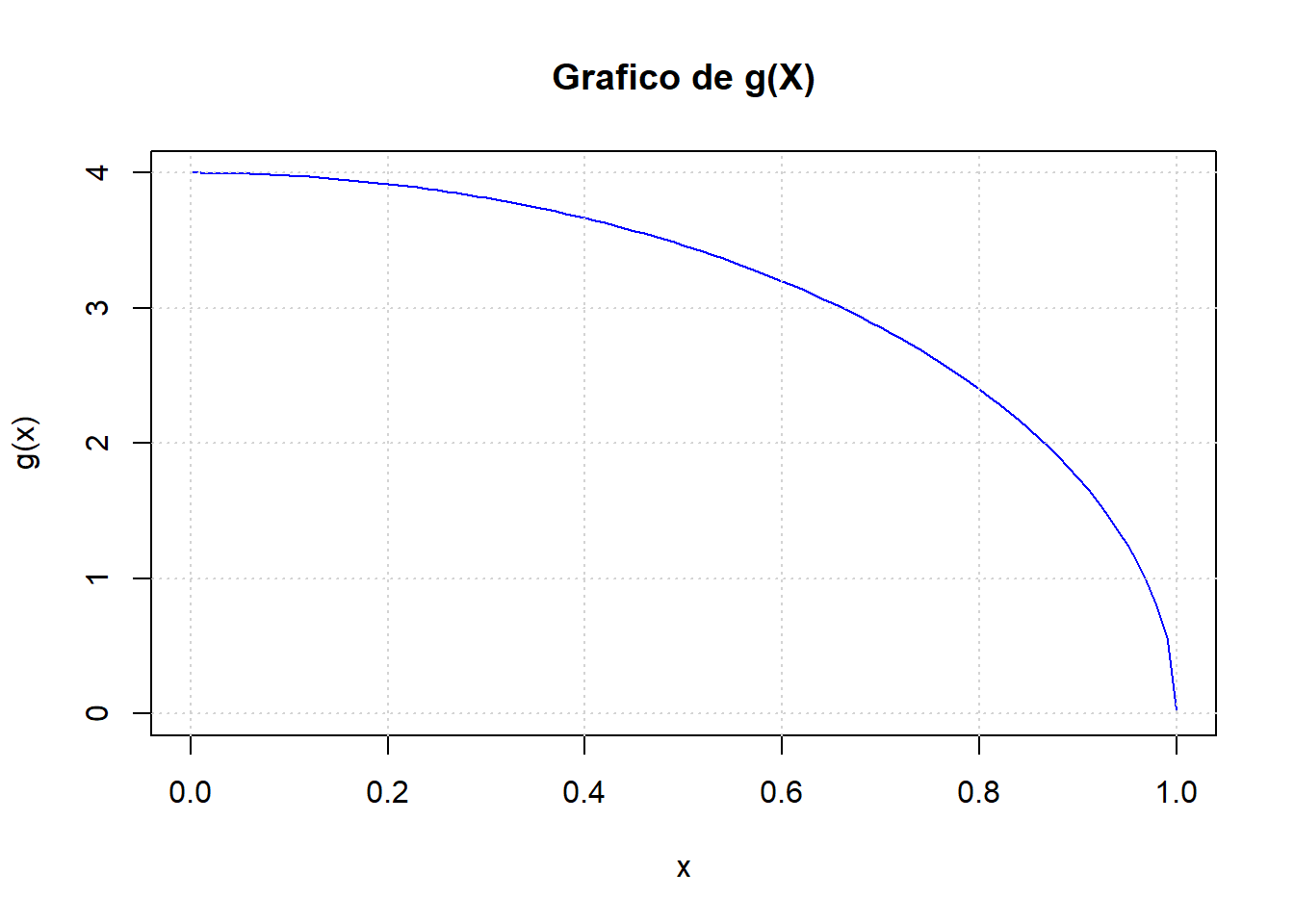
Podemos analizar la convergencia de la función \(\frac{1}{n}\sum g(u_i)\)
Y<-g(U) #genera el vector para cada observación
acumulado<-cumsum(Y)/(1:n)
plot(1:n,acumulado,col="blue",type="l",ylab="Aproximacion",xlab="Iteraciones")
abline(h=integrate(g,0,1)$value,col="red",lwd=1)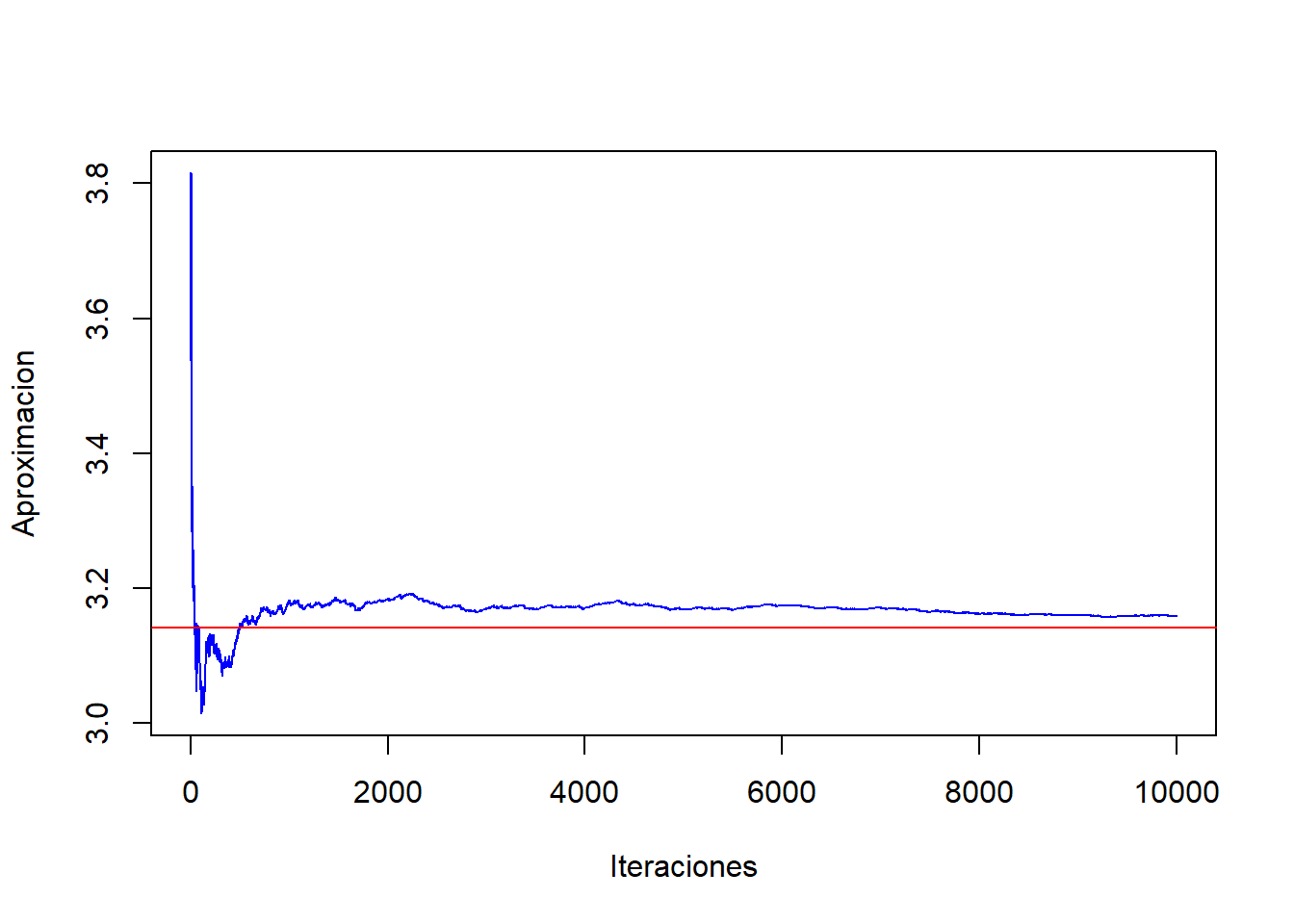
Si realizamos otra muestra de igual magnitud, los valores iniciales cambian pero siempre converge al valor
set.seed(1900)
n<-10^4 #Tamaño de la muestra
U2<-runif(n)
Y2<-g(U2) #genera el vector para cada observación
acumulado<-cumsum(Y2)/(1:n)
plot(1:n,acumulado,col="blue",type="l",ylab="Aproximacion",xlab="Iteraciones")
abline(h=integrate(g,0,1)$value,col="red",lwd=1.5)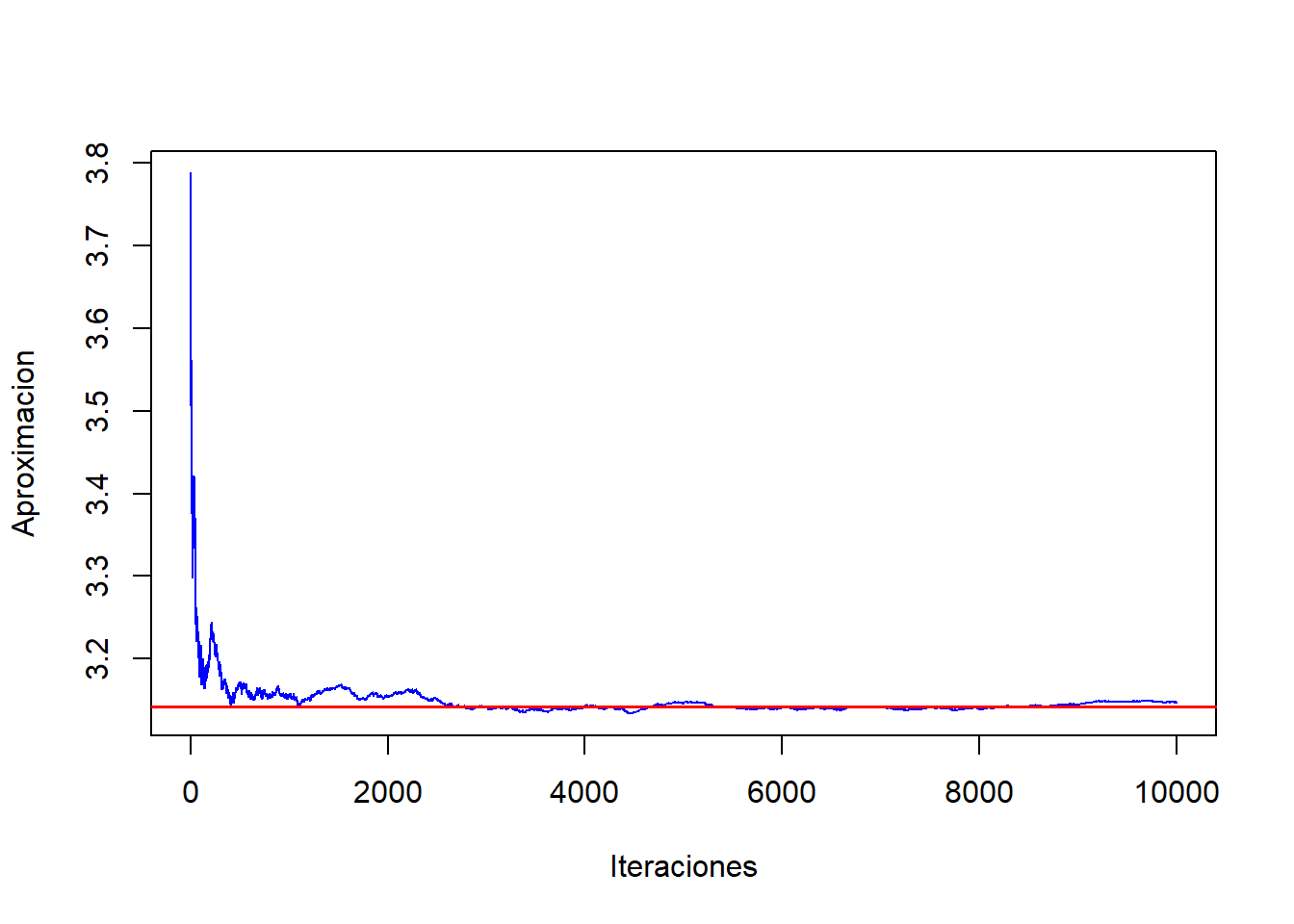
Para obtener el valor aproximado de \(\pi\)
P_est1=mean(Y)
P_est2=mean(Y2)
A<-matrix(c(P_est1,P_est2),ncol=2)
colnames(A) <- c("Estimacion 1", "Estimacion 2")
A Estimacion 1 Estimacion 2
[1,] 3.158386 3.147112El error absoluto de la estimación
e1<-(abs(P_est1-pi))
e2<-(abs(P_est2-pi))
A<-matrix(c(e1,e2),ncol=2)
colnames(A) <- c("Error 1", "Error 2")
A Error 1 Error 2
[1,] 0.01679344 0.005519002Si aumentamos las observaciones se disminuirá el error.\(\blacksquare\)
set.seed(2023)
n<-10^8 #Tamaño de la muestra
U3<-runif(n)
Y3<-g(U3) #genera el vector para cada observación
P_est3=mean(Y3)
e3=abs(P_est3-pi)
#estimación de error estandar
es1=sqrt(var(Y)/sqrt(10^4))
es2=sqrt(var(Y2)/sqrt(10^4))
es3=sqrt(var(Y3)/sqrt(10^8))
A<-matrix(c(P_est1,P_est2,P_est3,e1,e2,e3,es1,es2,es3),ncol=3, byrow=TRUE)
colnames(A) <- c("Caso 1", "Caso 2","Caso 3")
rownames(A) <- c("estimacion", "error absoluto","error estandar")
A Caso 1 Caso 2 Caso 3
estimacion 3.15838609 3.147111656 3.141574e+00
error absoluto 0.01679344 0.005519002 1.851218e-05
error estandar 0.08843538 0.088171683 8.926849e-03Algoritmo
- Generar una muestra \(U_1, U_2,..., U_n \sim U[a,b]\)
- Hacer \(X_i=U_i\)
- Hacer \(Y_i=g(X_i)\)
- Devolver \(I=(b-a) \displaystyle \sum_{i=1}^n \frac{Y_i}{n}\) \(\blacksquare\)
6.2 Muestreo por importancia
Una extensión inmediata de la integración de Montecarlo es el denominado Muestreo por Importancia. Este método es utilizado cuando deseamos obtener la esperanza matemática respecto a una densidad \(q(x)\) pero resulta que no es facil generar valores aleatorios de \(q(\cdot)\) y sin embargo, si es posible generar valores de \(x_i\) de una densidad \(\pi(x)\) “próxima” a \(q(\cdot)\). En tal caso:
\[\displaystyle \int_{a}^{b}f(x)q(x)dx=\int_{a}^{b}f(x)\left( \frac{q(x)}{\pi(x)}\right)\pi(x)dx \approx \frac{1}{n}\sum \frac{f(x_i)g(x_i)}{\pi(x_i)}\]
Donde los \(x_i\) son elegidos independientes de forma aleatoria de la densidad \(\pi(x_i)\) sobre el intervalo \((a,b)\).
Aunque podríamos utilizar cualquier función de importancia \(q\), este método tiene un comportamiento más adecuado cuando \(q(\cdot)\) es próxima a la verosimilitud.
6.2.1 Ejemplo 2
Estudiemos el caso de una función con dominio no acotado
\[\displaystyle \Phi(t)=\int_{t}^{\infty} \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\]
Consideremos el caso \(t=4.5\) empleando la integración por Montecarlo.
Al ser un intervalo no acotado, podemos realizar un cambio de variable:
\[y=\frac{1}{x+1} \rightarrow dy=-\frac{1}{(1+x)^2}dx=-y^2dy\]
Obtenemos la siguiente integral
\[\displaystyle \int_{t}^{\infty} \frac{1}{\sqrt{2\pi}}e^{-\frac{x2}{2}}dx=\int_{0}^{2/11} \frac{1}{\sqrt{2\pi}y^2}e^{-\frac{(1/y-1)^{-2}}{2}}dy\]
set.seed(2024)
n<-10^4 #Tamaño de la muestra
U<-runif(n,0,2/11)
g<-Vectorize(function(x) (exp(-((1/x-1)^(2))/2))/(sqrt(2*pi)*x^2))
Y<-(2/11)*g(U)
M<-matrix(c(mean(Y),pnorm(-4.5),abs(mean(Y)-pnorm(-4.5)),sqrt(var(Y)/sqrt(10^4))),ncol=4, byrow=TRUE)
colnames(M) <- c("Estimacion", "Valor Real","Error Absoluto","Error Estandar")
M Estimacion Valor Real Error Absoluto Error Estandar
[1,] 3.294373e-06 3.397673e-06 1.033004e-07 1.193555e-06Como se puede observar la integración por Montecarlo converge lento al valor, esto por el tamaño del área, para tener una aproximación más cercana se necesitaría una muestra de \(10^{5}\). \(\blacksquare\)
Por lo que podría usar una densidad auxiliar, como por ejemplo una exponencial de parametro \(\lambda = 1\) truncada en \(t\), es decir:
\[\pi(x) = \lambda e^{-\lambda (x-t)}, x>t\]
Generamos la muestra aleatoria con valores según la densidad auxiliar
set.seed(2024)
n<-10^4 #Tamaño de la muestra
A<-rexp(n)+4.5Construiremos nuestra función a integrar y estimaremos el resultado
g<-Vectorize(function(x) (exp(-((x)^(2))/2))/(sqrt(2*pi))/(exp(-x+4.5)))
Y2<-g(A)
M<-matrix(c(mean(Y2),pnorm(-4.5),abs(mean(Y2)-pnorm(-4.5)),sqrt(var(Y2)/sqrt(10^4))),ncol=4, byrow=TRUE)
colnames(M) <- c("Estimacion", "Valor Real","Error Absoluto","Error Estandar")
M Estimacion Valor Real Error Absoluto Error Estandar
[1,] 3.449627e-06 3.397673e-06 5.195359e-08 4.446724e-07Como podemos observar, para una muestra más pequeña la convergencia fue más rápida.
Nota:
En el caso de este ejemplo, y al ser distribuciones conocidas, podemos usar las funciones dnorm y dexp para la estimación de la función, obteniendo el mismo resultado.
w <- dnorm(A)/dexp(A - 4.5)
(mean(w))[1] 3.449627e-06La forma gráfica la aproximación es la siguiente:
plot(cumsum(Y2)/1:n, type = "l", ylab = "Aproximación", xlab = "Iteraciones")
abline(h=pnorm(-4.5), lty = 2)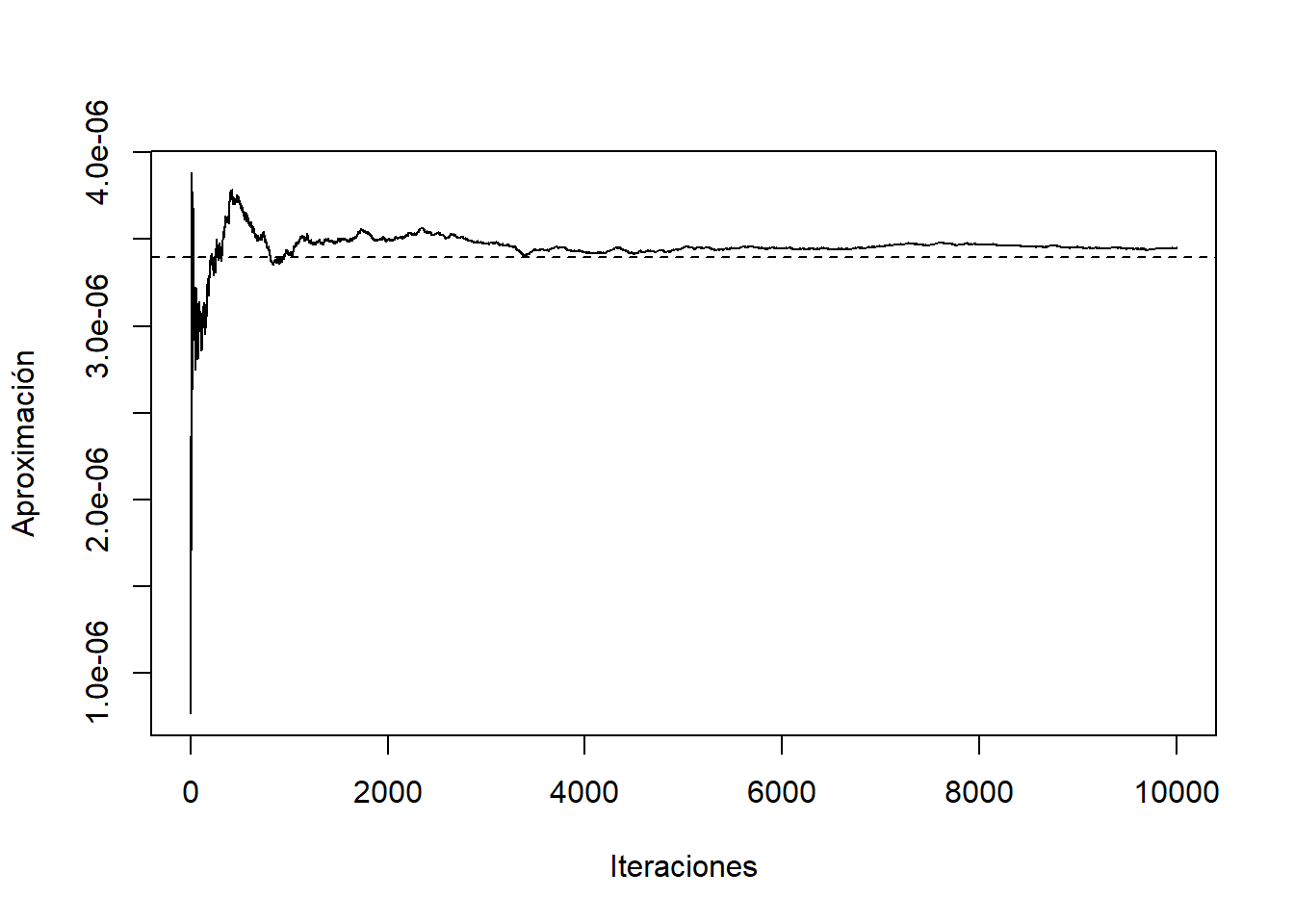
6.3 Método de Aceptación-Rechazo
Otro método habitualmente utilizado es el denominado Método de Aceptación-Rechazo. Este método consiste en generar una muestra de la distribución \(g(\theta)\), llamada envolvente, auxiliar o a priori, para generar una muestra de la distribución objetivo o a posteriori, tal que se verique:
\[\pi(\theta)L(\textbf{x}|\theta)<cg(\theta)\]
siendo \(c\) una constante positiva.
Algoritmo
Para genereración i-esima se tiene:
- Generar \(U_i, \sim U[a,b]\)
- Generar \(\theta_i \sim g(\cdot)\)
- Si \(c*U_i*g(\theta_i)<\pi(\theta_i)L(\textbf{x}|\theta_i)\) se acepta sino se rechaza y se regresa al punto 1. \(\blacksquare\)
6.3.1 Ejemplo 3
Para simular una variable de una función de densidad \(\beta(\alpha,\beta)\):
\[f(x)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}, 0\leq x \leq 1\]
Podemos considerar como distribución auxiliar envolvente una distribución \(U(0,1)\), con \(g(x)=1\) si \(0\leq x \leq 1\).
Para obtener la constante \(c\) debemos máximizar la función
\[c= max\left(\frac{f(x)}{g(x)}\right)\]
En particular la distribución beta es acotada y unimodal, y si \(\alpha,\beta >1\), su máximo se alcanza en la moda de la distribución, en el punto \(\frac{\alpha-1}{\alpha+\beta-2}\), y como nuestro \(g(x)=1\), el valor para la constante c, es el máximo que alcanza la función.
\[c=f \left( \frac{\alpha-1}{\alpha+\beta-2} \right)\]
Consideremos \(\alpha = 2 , \beta =4\), si comparamos la densidad objetivo la auxiliar reescalada (\(c*g(x)\)), podemos confirmar que está por encima
# densidad objetivo: dbeta
# densidad auxiliar: dunif
curve(dbeta(x, 2, 4), -0.1, 1.1, lwd = 2)
m <- dbeta((2 - 1)/(2 + 4 - 2), 2, 4)
# abline(h = m, lty = 2)
segments(0, m, 1, m, lty = 2, lwd = 2)
abline(v = 0, lty = 3)
abline(v = 1, lty = 3)
abline(h = 0, lty = 3)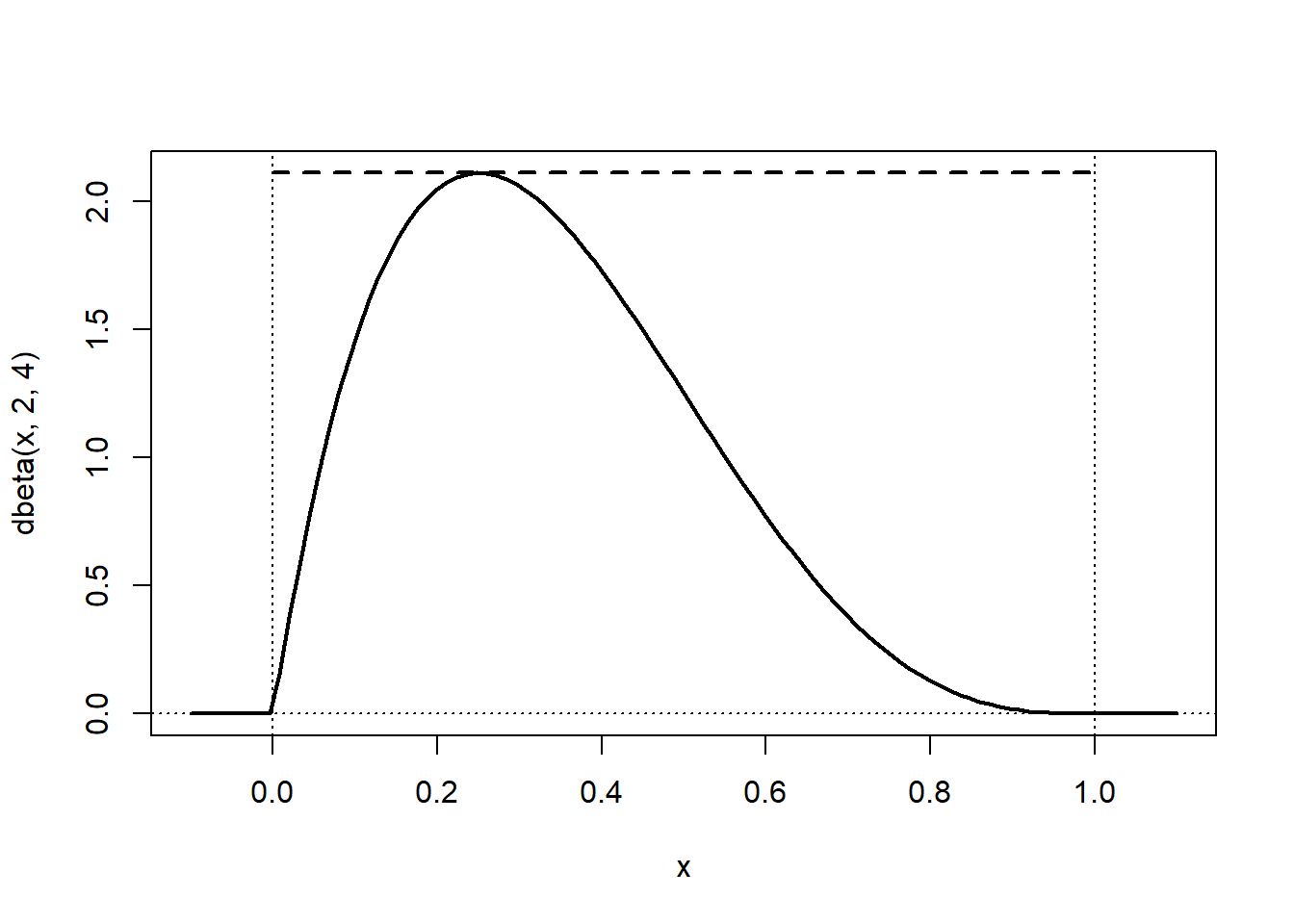
Aplicando el algoritmo de aceptación-rechazo tenemos:
#set.seed(2023)
U<-runif(10^4)
x<-runif(10^4,0,1)
ngen=length(x)
dbeta1=Vectorize(function(x) (20*x*(1-x)^3))
DIB<-dbeta1(x)
for(i in 1:10^4){
while((U[i]*m*1) >= (DIB[i])){ #sustituyo las rechazadas
U[i]=runif(1)
x[i]=runif(1)
DIB[i]<-dbeta1(x[i])
ngen=ngen+1}
}
ValorRes=dbeta1(x)Para analizar la eficiencia del algoritmo, podemos estimar la proporción de rechazos de la muestra original
{cat("Número de generaciones = ", ngen)
cat("\nNúmero medio de aceptados = ", ngen/10^4)
cat("\nProporción de rechazos = ", 1-10^4/ngen, "\n")}Número de generaciones = 21284
Número medio de aceptados = 2.1284
Proporción de rechazos = 0.5301635 Y también podemos representar la distribución de los valores generados y compararla con la densidad teórica. \(\blacksquare\)
hist(x, breaks = "FD", freq = FALSE, main = "")
curve(dbeta(x, 2, 4), col = 2, lwd = 2, add = TRUE)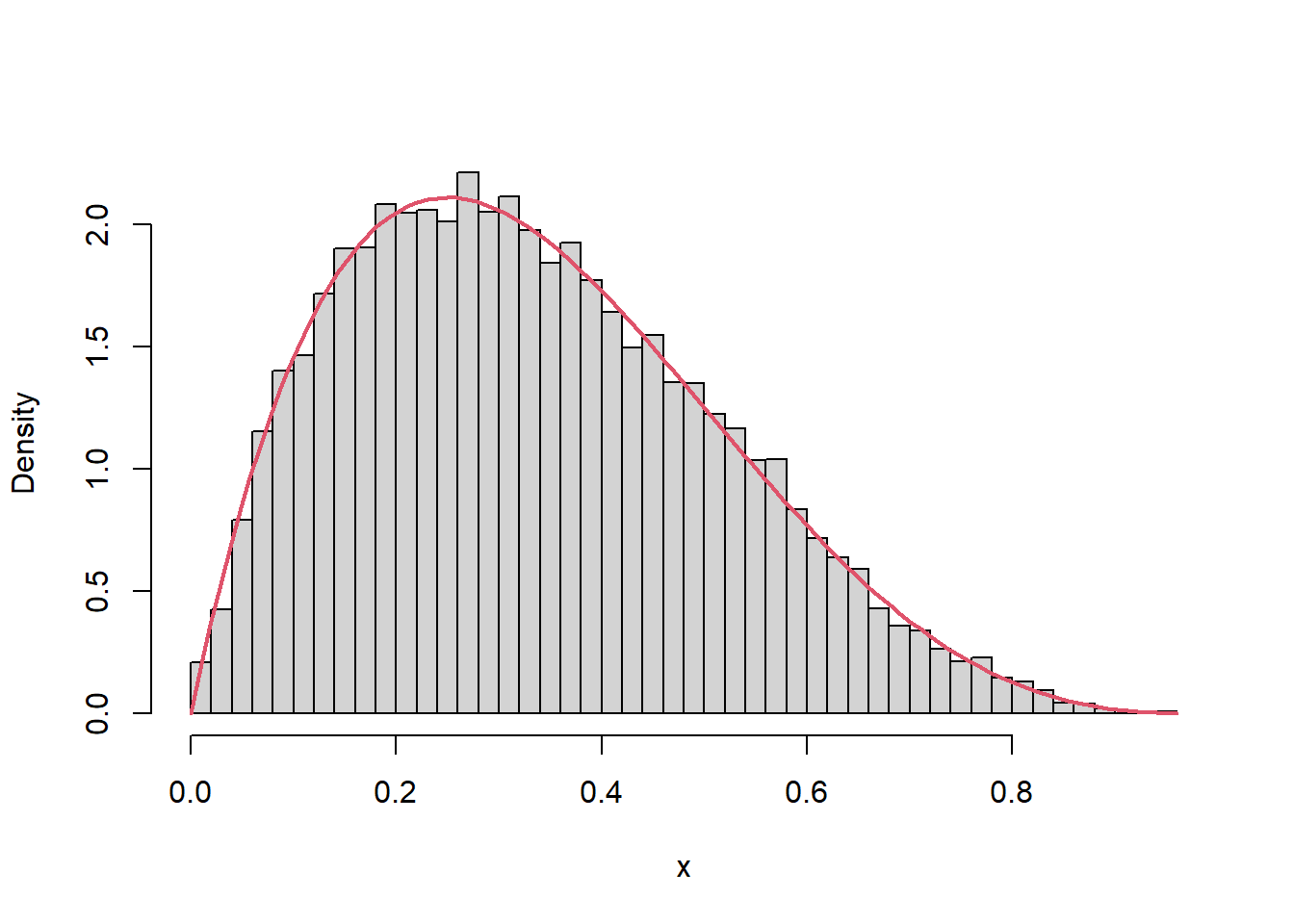
6.3.2 Ejemplo 4
Para la estimación bayesiana de la media de una normal se suele utilizar como distribución a priori una Cauchy.
Dada una muestra i.i.d. \(X_i \sim N(\theta_0,1)\) de tamaño \(n=100\) con \(\theta_0 \propto 1\). Utilizaremos una \(Cauchy(0,1)\) como distribución a priori y densidad auxiliar para simular por aceptación-rechazo una muestra de la densidad a posteriori.
Muestro algoritmo en el punto 3. cambia a:
\[c*U_i<L(\textbf{x}|\theta_i) \]
Tenemos como datos de la muestra:
mu0 <- 1
n <- 100
nsim <- 10^4
set.seed(54321)
mx <- rnorm(n, mean = mu0)Al ser una muestra debemos calcular su función de verosimilitud
lik <- Vectorize(function(mu) prod(dnorm(mx, mean = mu))) Para optener la constante c optima dada la muestra, sería el máximo de verosimilitud, que sabemos en este caso de la media con distribución normal, es el promedio \(\bar x\).
emv <- optimize(lik , int = range(mx), maximum = TRUE)Nota:
La funcion optimize nos permite optimizar numéricamente funciones, y brinda dos resultados, por defecto (default) minimiza, por lo que hay que indicarle que se debe maximizar.
- Maximum (minimum) el punto donde se alcanza el máximo (mínimo).
- Objective el punto crítico evaluado en la función.
emv$maximum[1] 0.9066271mean(mx)[1] 0.9066196c<-emv$objectiveObservemos el comportamiento de la distribución auxiliar de Cauchy, para esto usaremos una cuasi-función de densidad (omitiendo constantes)
f.cuasi <- function(mu) lik(mu)*dcauchy(mu)
curve(c * dcauchy(x), xlim = c(-4, 4), ylim = c(0, c/pi), lty = 2,
xlab = "mu", ylab = "cuasi-densidad")
curve(f.cuasi, add = TRUE)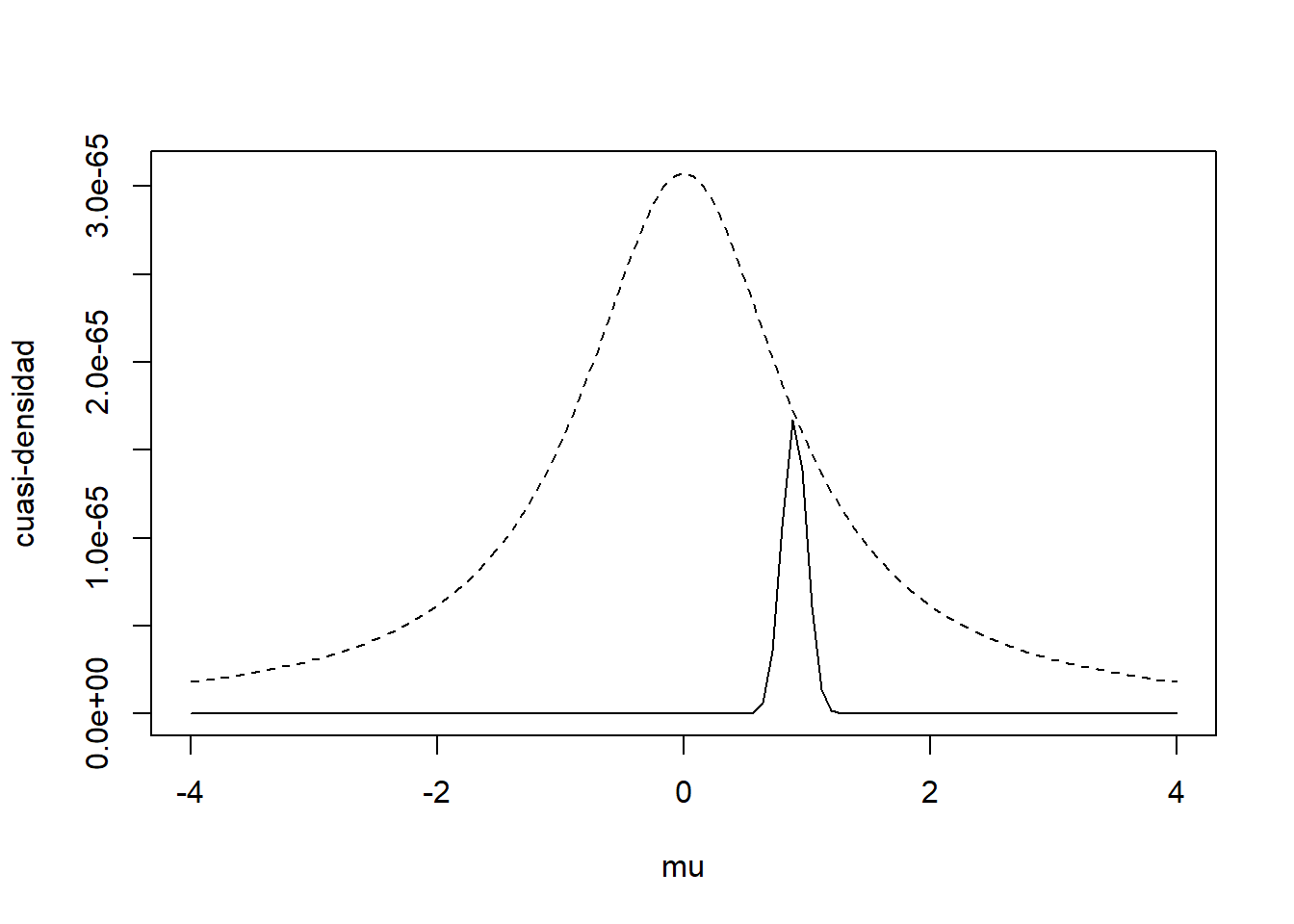
Observamos que la cuasi-densidad obtenida por \(\pi(\theta)L(\textbf{x}|\theta)\) recubre la función. Aplicando el algoritmo de aceptación-rechazo para obtener la distribución a posteriori.
U<-runif(nsim)
rc<-rcauchy(nsim)
ngen=length(rc)
Ver<-lik(rc)
for(i in 1:nsim){
while((U[i]*c) > (Ver[i])){
U[i]=runif(1)
rc[i]=rcauchy(1)
Ver[i]<-lik(rc[i])
ngen=ngen+1}
}
Valorres=lik(rc)Para analizar la eficiencia del algoritmo
{cat("Número de generaciones = ", ngen)
cat("\nNúmero medio de generaciones = ", ngen/nsim)
cat("\nProporción de rechazos = ", 1-nsim/ngen, "\n")}Número de generaciones = 229892
Número medio de generaciones = 22.9892
Proporción de rechazos = 0.9565013 Como utilizamos una cuasi-función de densidad, debemos ajustarla por la constante c entre el valor medio de la generaciones.
cte <- c*nsim/ngen
f.aprox <- function(rc) f.cuasi(rc)/ctePodemos aproximar un intervalo de credibilidad, tomando los cuantiles respectivos, por ejemplo para un IC al 95% podemos:
q <- quantile(rc, c(0.025, 0.975))
q 2.5% 97.5%
0.7022693 1.0865752 En el gráfico siguiente,podemos observar el estimador y IC de Bayes:
hist(rc, freq=FALSE, main="",breaks="FD")
# abline(v = mean(x), lty = 3) # Estimación frecuentista
abline(v = mean(rc), lty = 2, lwd = 2) # Estimación Bayesiana
abline(v = q, lty = 2)
curve(f.aprox, col = "blue", add = TRUE)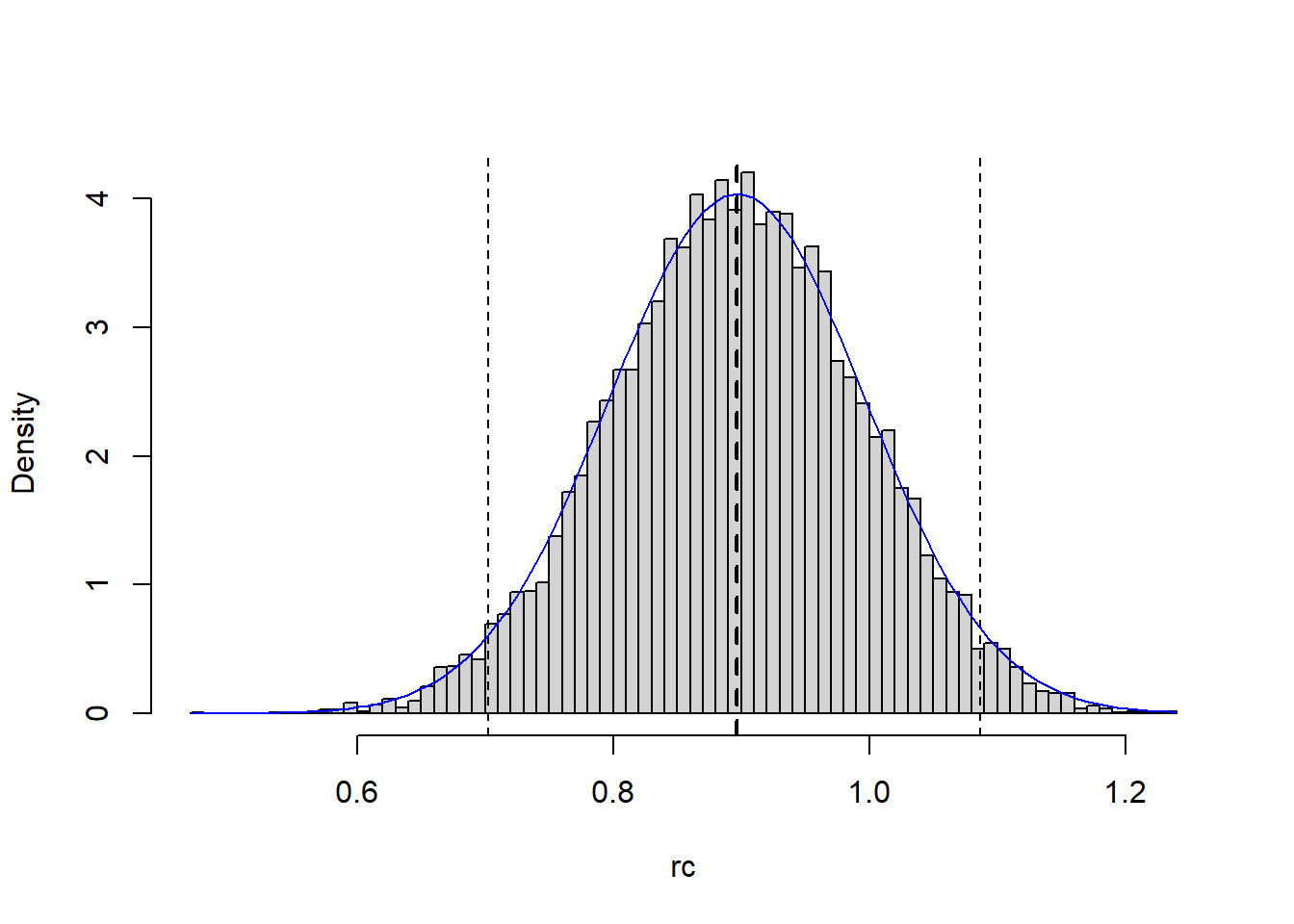
6.3.3 Ejemplo 5
Para simular una función
\[f(x)=\left(\frac{2x}{e^x} \right)^2, si \quad x\geq0\]
Podemos considerar como distribución auxiliar envolvente una distribución \(Exp(1)\), con \(g(x)=e^{-1}\) si \(0\leq x\).
Grafiquemos nuestra función \(f(x)/g(x)\)
faux=function(x){(2*x/exp(x))^2/dexp(x,1)}
curve(faux(x),0,10)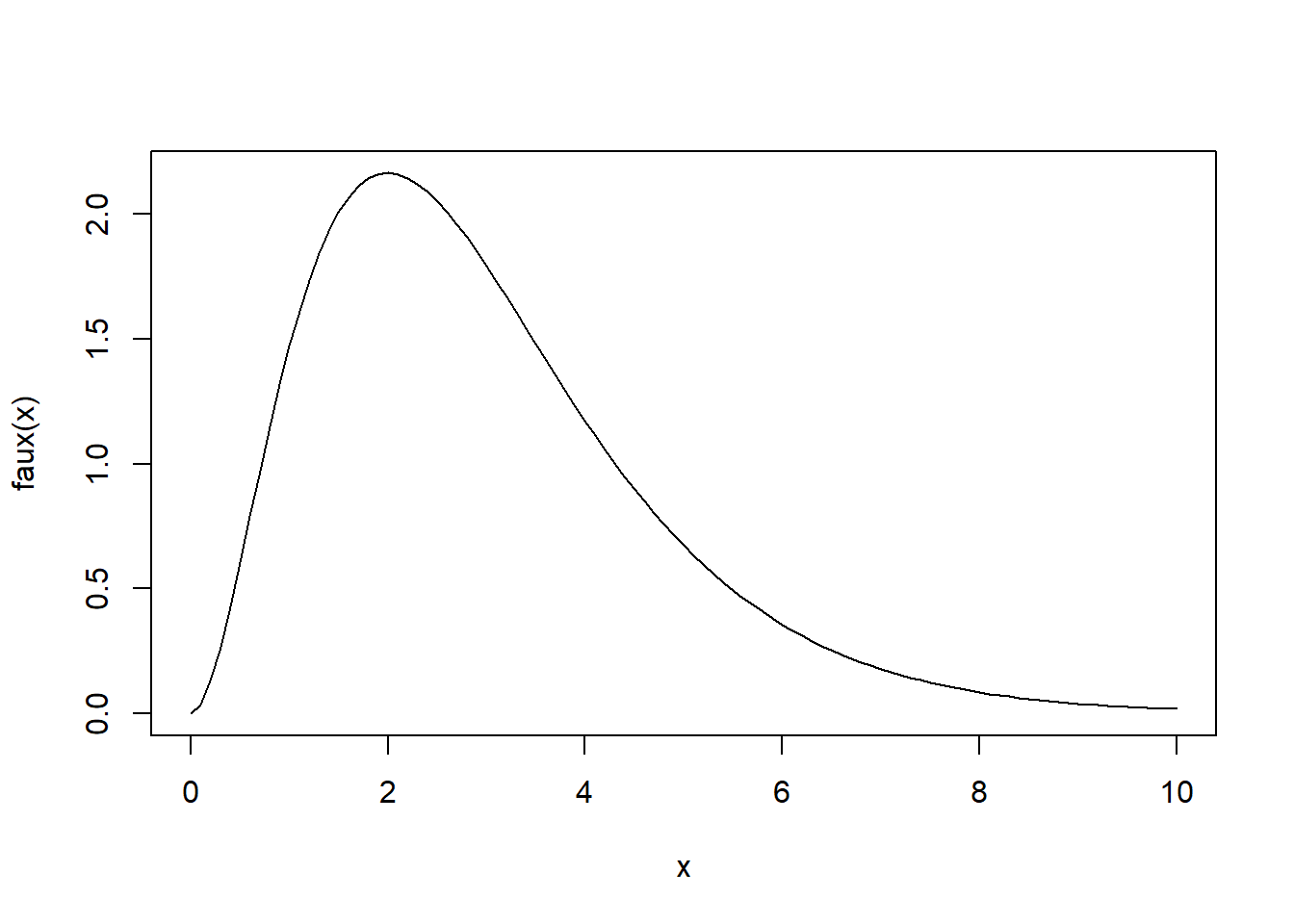
Observemos que la función es acotada y que alcanza un máximo entre \([0,4]\), como en los otros ejemplos debemos encontrar el máximo de nuestra función a simular
c_opt = optimize(faux, maximum=TRUE, interval=c(0,4))
c <- c_opt$objective
cat("máximo \n")máximo c[1] 2.165365Aplicando el algoritmo de aceptación-rechazo tenemos:
n=10^4
U<-runif(n,0,1)
x.aux<-rexp(n,1)
ngen=n
f<-function(x) (2*x/exp(x))^2
fx<-f(x.aux)
for(i in 1:n){
while(U[i]*c*dexp(x.aux[i],1) >= fx[i]){ #sustituyo las rechazadas
U[i]<-runif(1,0,1)
x.aux[i]<-rexp(1,1)
fx[i]<-f(x.aux[i])
ngen=ngen+1}
} Para analizar la eficiencia del algoritmo, podemos estimar la proporción de rechazos de la muestra original
cat("Número de generaciones = ", ngen)Número de generaciones = 21505cat("\nNúmero medio de aceptados = ", ngen/n)
Número medio de aceptados = 2.1505cat("\nProporción de rechazos = ", 1-n/ngen, "\n")
Proporción de rechazos = 0.5349919 Y también podemos representar la distribución de los valores generados y compararla con la densidad teórica. \(\blacksquare\)
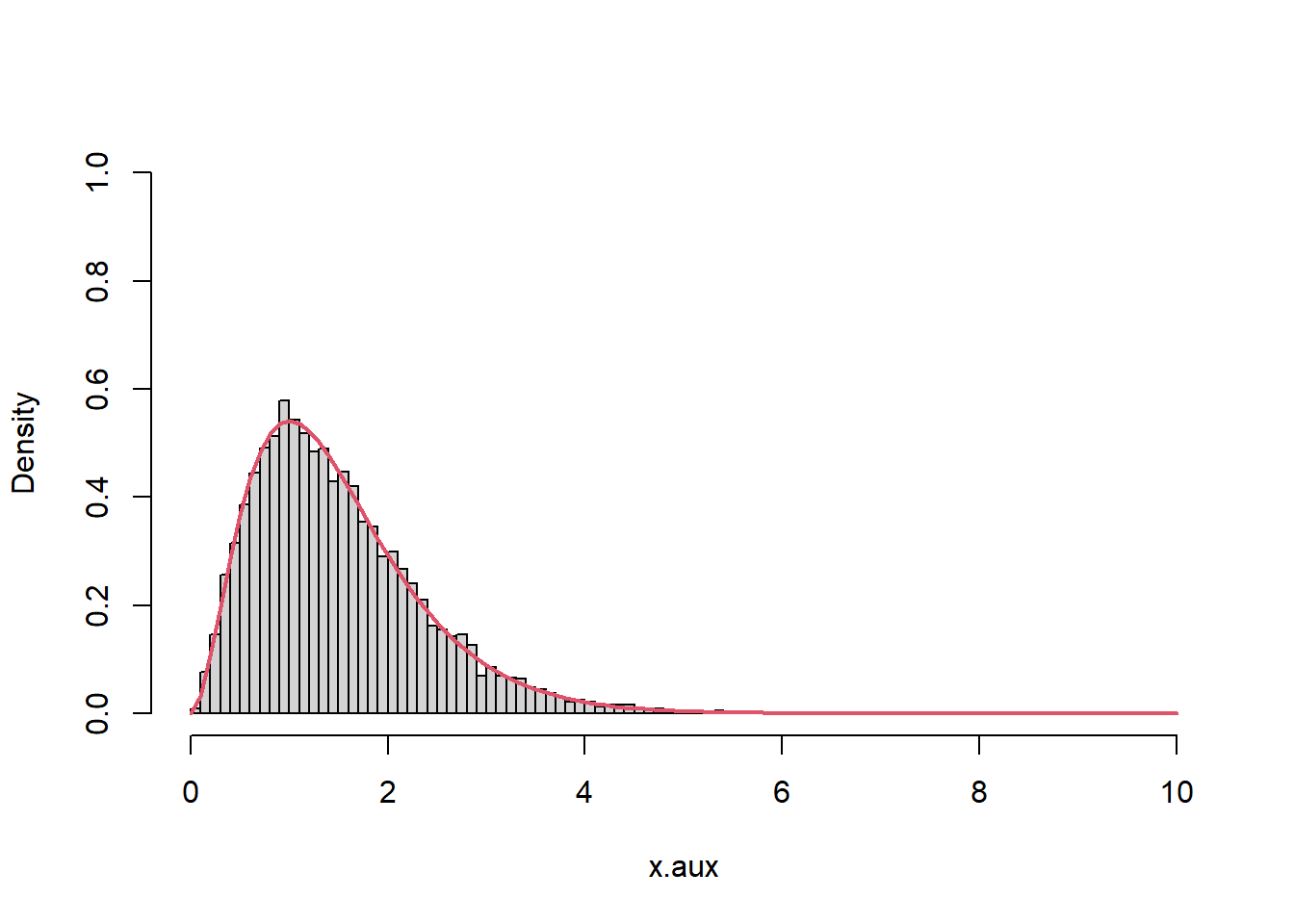
hist(x.aux, freq = FALSE, main = "",breaks="FD",xlim=c(0,10),ylim=c(0,1))
curve(f(x), col = 2, lwd = 2,0,10, add = TRUE)