10 Cópulas Arquimedianas Cap. 4
10.1 Cópulas Arquimedianas
En esta sección nos centraremos en encontrar Cópulas que cumplan con la siguiente ecuación:
\[\varphi(C(u,v))=\varphi(u)+\varphi(v)\]
Esta función \(\varphi\) se llamará función generadora o generatriz de la Cópula \(C\), ahora bien para poder “despejar” la Cópula \(C(u,v)\) requerimos de una función inversa.
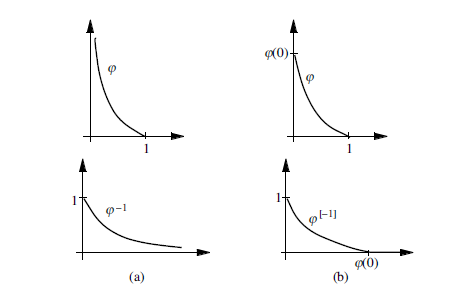
Definición
Sea \(\varphi: \mathbb{I} \to [0,\infty]\) una función continua, estrictamente decreciente, tal que \(\varphi(1)=0\). La pseudo-inversa de \(\varphi\) es la función \(\varphi^{[-1]}:[0,\infty]\to\mathbb{I}\) tal que:
\[ \varphi^{[ -1 ]} = \begin{cases} \varphi^{-1} & 0 \leq t \leq \varphi(0) \\ 0 & \text{en otro caso} \end{cases} \] Observe que \(\varphi \left(\varphi^{[ -1 ]}(t) \right)=\min(t,\varphi(0))\), además, si \(\varphi (0) = \infty \Rightarrow \varphi^{-1}\)
A partir de la definición anterior, podemos escribir:
\[C(u,v)=\varphi^{[ -1 ]}(\varphi(u)+\varphi(v))\] Lema
Sea \(\varphi: \mathbb{I} \to [0,\infty]\) una función continua, estrictamente decreciente, tal que \(\varphi(1)=0\), Entonces la función \(C: \mathbb{I}^2\to\mathbb{I}\) definida por:
\[C(u,v)=\varphi^{[ -1 ]}(\varphi(u)+\varphi(v))\] cumple las primeras condiciones de las Cópulas, es decir las condiciones de borde
Prueba:
\(C(0,v)=\varphi^{[ -1 ]}(\varphi(0)+\varphi(v))\), dado que \(\varphi(0)+\varphi(v)\geq \varphi(0)\), entonces por la definición de \(\varphi^{[ -1 ]}\), \(C(0,v)=0\).
\(C(1,v)=\varphi^{[ -1 ]}(\varphi(1)+\varphi(v))=\varphi^{[ -1 ]}(\varphi(v))=v\)
Similar para los casos \(C(u,0)\) y \(C(u,1)\).
Nota
Como \(\varphi^{[-1]},\varphi(1)\) son continuas, entonces \(C\) es continua y posee dominio en \(\mathbb{I}^2\)
Lema
Sea \(\varphi: \mathbb{I} \to [0,\infty]\) una función continua, estrictamente decreciente, tal que \(\varphi(1)=0\), Entonces la función \(C: \mathbb{I}^2\to\mathbb{I}\) definida por: \(C(u,v)=\varphi^{[ -1 ]}(\varphi(u)+\varphi(v))\).
Entonces C es 2-creciente si sólo si para todo \(v \in \mathbb{I}\), tal que \(u_1 \leq u_2\), entonces:
\[C(u_2,v)-C(u_1,v)\leq u_2-u_1\]
Prueba
Si \(C\) es 2-creciente entonces \(V_C([u_1,u_2]\text{x}[v,1])\geq 0\)
\[V_C([u_1,u_2]\text{x}[v,1])=C(u_1,v)-C(u_1,1)-C(u_2,v)+C(u_2,1)\geq 0\]
\[\Rightarrow C(u_1,v)-u_1-C(u_2,v)+u_2 \geq 0\] Tomemos \(v_1, v_2 \in \mathbb{I}\) tal que \(v_1 \leq v_2\). Observe que \(C(0,v_2)=0\leq v_1 \leq v_2 =C(1,v_2)\), como \(C\) es continua, implica que existe un \(t \in \mathbb{I}\) tal que: \(C(t,v_2)=v_1 \rightarrow \varphi(C(t,v_2))=\varphi(v_1)=\varphi(t)+\varphi(v_2)\)
\[C(u_2,v_1)-C(u_1,v_1)=\varphi^{[ -1 ]}(\varphi(u_2)+\varphi(v_1))-\varphi^{[ -1 ]}(\varphi(u_1)+\varphi(v_1))\] \[=\varphi^{[ -1 ]}(\varphi(u_2)+\varphi(t)+\varphi(v_2))-\varphi^{[ -1 ]}(\varphi(u_1)+\varphi(t)+\varphi(v_2))\] \[=C(C(u_2,v_2),t)-C(C(u_1,v_2),t)\leq C(u_2,v_2)-C(u_1,v_2)\] \[\Rightarrow C(u_2,v_1)-C(u_1,v_1)\leq C(u_2,v_2)-C(u_1,v_2) \Rightarrow 0 \leq V_C([u_1,u_2]\text{x}[v_1,v_2])\]
Teorema
Sea \(\varphi:\mathbb{I} \to [0,\infty]\) función continua, estrictamente decreciente, tal que \(\varphi(1)=0\) y sea \(\varphi^{[-1]}\) seudo-inversa de \(\varphi\). Entonces la función \(C:\mathbb{I}^2\to\mathbb{I}\), definida como:
\[C(u,v)=\varphi^{[ -1 ]}(\varphi(u)+\varphi(v))\] es una Cópula si y sólo si \(\varphi\) es convexa.
Prueba
Leer prueba en la página 111 del libro.
Definición
Las Cópulas que cumple el Teorema anterior, se llaman Cópulas Arquimedianas.
La función \(\varphi\) se le llama función generadora de la Cópula.
Si \(\varphi(0)=\infty\), se dice que es Función Estrictamente Generadora, y en este caso \(\varphi^{[ -1 ]}=\varphi^{-1}\) y \(C(u,v)=\varphi^{ -1 }(\varphi(u)+\varphi(v))\) y la Cópula generada, se dice que es Cópula Estrictamente Arquimediana.
La función \(\varphi\) se le llama también generador aditivo de \(C\). Si definimos a \(\lambda(t)=exp(-\varphi(t))\) y \(\lambda^{[-1]}(t)=\varphi^{[-1]}(-ln(t))\), entonces:
\[C(u,v)=\lambda^{[-1]}[\lambda(u)\lambda(v)]\] la función \(\lambda\) se le llama generador multiplicativo.
Ejemplo 1
Sea \(\varphi(t)=-ln(t)\) con \(t \in [0,1]\). Cómo \(\varphi(0)=\infty\), entonces es estricta. Entonces \(\varphi(t)^{-1}=e^{-t}\). Analicemos la Cópula resultante:
\[C(u,v)=\varphi^{-1}(\varphi(u)+\varphi(v))=e^{-(-ln(u)-ln(v))}=e^{ln(uv)}=uv=\Pi(u,v)\]
Es decir la Cópula \(\Pi\) es una Cópula Estrictamente Arquimediana.
Ejemplo 2
Sea \(\varphi(t)=1-t\) con \(t \in [0,1]\). Cómo \(\varphi^{[-1]}(t)=1-t\) para \(t \in [0,1]\) y 0 si \(t>1\), es decir \(\varphi^{[-1]}(t)=max(1-t,0)\). Entonces:
\[C(u,v)=\varphi^{-1}(\varphi(u)+\varphi(v))=max(1-((1-u)+(1-v)),0)=max(u+v-1,0)=W(u,v)\]
Es decir la Cópula \(W\) es una Cópula Arquimediana.
Nota
La Cópula \(M(u,v)=min(u,v)\) no es Arquimediana.
Ejemplo 3
Sea Sea \(\varphi_{\theta}(t)=ln(1-\theta ln(t))\) con \(t \in (0,1]\), observe que \(\varphi_{\theta}(0)=\infty\), es decir \(\varphi_{\theta}(t)\) es estricta y \(\varphi(t)^{-1}=e^{(1-e^t)/\theta}\). Entonces
\[C(u,v)=\varphi^{-1}(\varphi(u)+\varphi(v))=uve^{-\theta ln(u)ln(v)}\]
Que es la Cópula de Sobrevivencia de una distribución Gumbel bivariada exponencial.
Teorema
Sea \(C\) una Cópula Arquimediana con función generadora \(\varphi\). Entonces:
\(C\) es simétrico, es decir \(C(u,v)=C(v,u)\) para todo \(u, v \in \mathbb{I}\)
\(C\) es asociativa, es decir \(C(C(u,v),w)=C(u,C(v,w))\) para todo \(u, v,w \in \mathbb{I}\)
Si \(c>0\) constante, entonces \(c\varphi\) es también función generadora de \(C\).
Prueba
\(C(u,v)=\varphi^{[-1]}(\varphi(u)+\varphi(v))=C(v,u)\)
\(C(C(u,v),w)=\varphi^{[-1]}(\varphi(C(u,v))+\varphi(w))=\varphi^{[-1]}(\varphi(\varphi^{[-1]}(\varphi(u)+\varphi(v)))+\varphi(w))\)
Por la definición de \(\varphi(\varphi^{[-1]})\), tenemos que:
\(C(C(u,v),w)=\varphi^{[-1]}(min(\varphi(u)+\varphi(v),\varphi(0))+\varphi(w))\)
\(C(C(u,v),w)=\varphi^{[-1]}(min(\varphi(u)+\varphi(v)+\varphi(w),\varphi(0)+\varphi(w)))\),
Observe que en caso que el mínimo sea \(\varphi(0)+\varphi(w)\) como \(\varphi(0) \leq \varphi(0)+\varphi(w)\) implica que \(\varphi^{[-1]}(\varphi(0)+\varphi(w))=\varphi^{[-1]}(\varphi(0))\),
tenemos que:
\(\varphi^{[-1]}(min(\varphi(u)+\varphi(v)+\varphi(w),\varphi(0)+\varphi(w)))=\varphi^{[-1]}(min(\varphi(u)+\varphi(v)+\varphi(w),\varphi(0)))\)
Bajo un razonamiento similar al anterior podemos llegar a que:
\(\varphi^{[-1]}(min(\varphi(u)+\varphi(v)+\varphi(w),\varphi(0)))=\varphi^{[-1]}(min(\varphi(u)+\varphi(v)+\varphi(w),\varphi(0)+\varphi(u)))=\varphi^{[-1]}(min(\varphi(v)+\varphi(w),\varphi(0))+\varphi(u))=C(u,C(v,w))\)
- Definamos \(\psi=c \varphi\), como \(\varphi\) es función generadora y \(c>0\) entonces \(\psi\) cumple con las hipótesis del teorema, por lo que existirá una Cópula Arquimediana \(\hat C\) con función generadora \(\psi\),
\[C(u,v) = \varphi^{[-1]}(\varphi(u)+\varphi(v)) \iff\]
\[\varphi(C(u,v))=\varphi(u)+\varphi(v)\iff\]
\[c\varphi(C(u,v))=c\varphi(u)+c\varphi(v)\iff\]
\[C(u,v)=\psi^{[-1]}(\psi(u)+\psi(v)))=\hat C(u,v)\]
Nota
Si \(C\) es una Cópula asociativa tal que la seccional diagonal \(\delta_C(u)<u\) para todo \(u \in (0,1)\). Entonces \(C\) es Arquimediana.
10.2 Familias Arquimedianas de 1 o 2 parámetros.
Muchas funciones generadoras \(\varphi\) de Cópulas Arquimedianas posee un parámetro \(\theta\), el cuál usualmente representa el grado de dependencia entre las variables. El conjunto de Cópulas que genera una función \(\varphi_\theta(t)\) se llama familia.
Los extremos del dominio de \(\theta\) se denominan Casos límites o Casos Especiales.
Ejemplo
Consideremos la función generadora: \[\varphi_\theta(t)=\frac{1}{\theta}(t^{-\theta}-1)\]
Analizaremos los casos donde la función \(\varphi_\theta(t)\) existe y es convexa:
La función \(\varphi_\theta(t)\) existe para todo \(\theta \in \mathbb{R}-\{0\}\)
Analicemos el caso donde \(\varphi_\theta(t)\) es decreciente tenemos que:
\[\varphi'_\theta(t)=-t^{-(\theta+1)}\] observe que dado que \(t \in [0,1]\) para cualquier \(\theta \in \mathbb{R}-\{0\}\), se tiene que \(\varphi'_\theta(t)\leq 0\), por ende la función \(\varphi_\theta(t)\) es decreciente o al menos no creciente.
También necesitamos que \(\varphi_\theta(t)\) sea convexa, es decir que \(\varphi''_\theta(t)\geq0\).
\[\varphi''_\theta(t)=(\theta+1)t^{-(\theta+2)}\] Por lo que \(\varphi_\theta(t)\) es convexa si \(\theta \geq -1\). Entonces \(\varphi_\theta(t)\) es una función generadora de Cópulas si \(\theta \in [-1,\infty)-\{0\}\).
Observe que si \(\theta<0\) entonces \(\varphi_\theta(0)=-1/\theta\) y si \(\theta\geq 0\) entonces \(\varphi_\theta(0)=\infty\), es decir para los casos donde \(\theta\geq 0\) la función es estrictamente generadora.
Construiremos la Cópula generada por \(\varphi_\theta(t)\), definamos la pseudo-inversa de \(\varphi_\theta(t)\)
\[ \varphi^{[-1]}_\theta(t)=\begin{cases} (\theta t+1)^{-1/\theta} & 0\leq t \leq \varphi_\theta(0) \\ 0 & \text{en otro caso} \end{cases} \] Por lo que la Cópula generada será
\[ C(u,v)=\varphi^{[-1]}_\theta(\varphi_\theta(u)+\varphi_\theta(v))=\begin{cases} (u^{-\theta}+v^{-\theta}-1)^{-1/\theta} & 0\leq \varphi_\theta(u)+\varphi_\theta(v) \leq \varphi_\theta(0) \\ 0 & \text{en otro caso} \end{cases} \]
La desigualdad \(0\leq \varphi_\theta(u)+\varphi_\theta(v) \leq \varphi_\theta(0)\) nos genera una condición fuerte sobre la Cópula, pero si analizamos podemos extender la solución al caso \(1\leq \varphi_\theta(u)+\varphi_\theta(v)\) generando una condición más débil para la existencia de la Cópula, donde se define que sea real para cualquier \(\theta\). Por lo que podemos simplificar la expresión a:
\[C_{\theta}(u,v)=\left[max(u^{-\theta}+v^{-\theta}-1,0)\right]^{-1/\theta}\]
Los extremos de \(\theta\) en este caso los límites y casos especiales sería tres: \(\theta=-1,0,\infty\)
\[C_{-1}(u,v)=max(u+v-1,0)=W(u,v)\]
\[C_{0}(u,v) =\Pi(u,v)\]
\[C_{\infty}(u,v)=M(u,v)\]
ver tabla y gráficos de un parámetro \(\theta\) página 116-122
Una propiedad interesante de las cópulas arquimedianas es que dada una función generadora \(\varphi\), podemos generar una familia de funciones generadoras de uno o dos parámetros \(\alpha\) y \(\beta\).
Recordemos que si \(f\) una función real convexa de dominio \(A\) y \(g\) una función real convexa no decreciente con domino \(B\), donde \(A\) y \(B\) son conjuntos convexos tal que \(f(A)\subset B\) entonces \(g \circ f\) es convexa.
Proposición
Sea \(\varphi(t)\) una función generadora de una Cópula arquimediana. Entonces:
\(\varphi_{\alpha,1}(t)=\varphi(t^\alpha)\) con \(\alpha \in (0,1]\), es una funcion generadora de una Cópula Arquimediana. (Potencia interior)
\(\varphi_{1, \beta}(t)=(\varphi(t))^\beta\) con \(\beta \in [1,\infty)\), es una funcion generadora de una Cópula Arquimediana. (Potencia Exterior)
\(\varphi_{\alpha, \beta}(t)=(\varphi(t^\alpha))^\beta\) con \(\alpha\) y \(\beta\) definidos anteriormente, es una funcion generadora de una Cópula Arquimediana.
Definición
Para cualquier \(u \in \mathbb{I}\) podemos definir la n-enesima Potencia-C (\(u_C^n\)) de \(u\) como:
\[u_C^{n}=C(u,u_C^{n-1})\quad u^1_C=u\]
observe que \(u^2_C=\delta_C(u)\) la seccional diagonal de \(C\), esta definición permite enunciar una versión del Axioma de Arquimides ( dado \(x>0\), \(y\) un número real, existe un \(n \in \mathbb{N}\) tal que \(nx>y\)), de ahí el nombre de esta Cópulas. Se puede demostrar que para cualquier \(u,v \in \mathbb{I}\) existe un entero positivo \(n\) tal que: \(u^n_C<v\)
Definición
Una función \(f\) definida en \([0,\infty)\) se dice que es subaditiva si para todo x,y se cumple que:
\[f(x+y)\leq f(x)+f(y)\]
Teorema
Sea \(\varphi\) una función generadora de Cópulas arquimedianas. Asumiremos que \(\varphi_{\alpha,1}\) y \(\varphi_{1,\beta}\) generan Cópulas \(C_{\alpha,1}\) y \(C_{1,\beta}\) respectivamente.
Si \(1\leq \beta_1\leq \beta_2\) entonces \(C_{1,\beta_1} \prec C_{1,\beta_2}\).
Si \(\varphi\left([\varphi^{[-1]}(t)]^\theta \right)\) es subaditiva, entonces \(\alpha_1\leq \alpha_2\) implica que \(C_{\alpha_1,1} \prec C_{\alpha_2,1}\)
Como vemos la familias de potencia exterior genera Cópulas positivamente ordenadas, pero con potencias interiores no es cierto, y en general no son familias ordenadas.
Si al Teorema anterior le agregamos la hipótesis que si \(\varphi'_{\alpha,1}/\varphi_{\alpha,1}\) es no decreciente con respecto a \(\alpha\), entonces si \(\alpha_1 \leq \alpha_2\) implica que \(C_{\alpha_1,1} \prec C_{\alpha_2,1}\).
Teorema
Sea \(\varphi\) una función generadora de Cópulas arquimedianas. Asumiremos que \(\varphi_{\alpha,1}\) y \(\varphi_{1,\beta}\) generan Cópulas \(C_{\alpha,1}\) y \(C_{1,\beta}\) respectivamente.
- Si \(\varphi\) es continuamente diferenciable y \(\varphi'(1) \neq 0\) Entonces:
\[C_{0,1}(u,v)=\lim_{\alpha\to 0^+}C_{\alpha,1}(u,v)=\Pi(u,v)\]
- \(C_{1,\infty}(u,v)=\lim_{\beta \to \infty}C_{1,\beta}(u,v)=M(u,v)\)
Ejercicios pág 132-135. 150( del tema analizado)
10.3 Cópulas Elipticas
Sea \(X\) un vector aleatorio se dice que tiene una distribución eliptica (\(\mathcal{E}(\mu,\Sigma,g)\)) con media \(\mu \in \mathbb{R}^n\) y matriz de Covarianzas \(\Sigma=\sigma_{ij} \in \mathbb{M}(n,n)\), y una función \(g:[0,\infty)\to [0,\infty)\) conocida como generadora si \(X\) se puede expresar como:
\[X=\mu+RAU\]
donde \(AA^t=\Sigma\) las descomposición de Cholesky de \(\Sigma\), \(U\) un vector aleatorio con distribución uniforme en la esfera unidad \(\mathbb{S}=\{u_1^2+\cdots u_n^2=1\}\) y \(R\) una variable aleatoria positiva independiente de \(U\), con densidad para todo \(r>0\)
\[f_g(r)=\frac{2\pi^{n/2}}{\Gamma(n/2)}r^{n-1}g(r^2)\]
Si Existe la función de densidad de \(X\sim \mathcal{E}(\mu,\Sigma,g)\), es de la forma:
\[h_g(X)=|\Sigma|^{-1/2}g((x-\mu)^t\Sigma(x-\mu))\]
Si tomamos \(g(t)=(2\pi)^{n/2}exp(-t/2)\) entonces \(X\) tiene como distribución una Normal Multivariada.
Si tomamos \(g(t)=c(1+t/\nu)^{-(n+\nu)/2}\), con \(c\) una constante adecuada, entonces \(X\) tiene como distribución una t-student multivariada con \(\nu\) grados de libertad.
Una de las características de las distribuciones elipticas es que su componentes: \(X_1/\sqrt{\sigma_{11}},\cdots, X_n/\sqrt{\sigma_{nn}}\) son identicamente distribuidos de acuerdo con función de distribución \(F_g\).
Este hecho, como se mencionó anteriormente es una limitación para modelar problemas estocásticos que sus componentes no son similares, para evitar este problema podemos calcular una Cópula de distribuciones elípticas y utilizarla con algunas distribuciones marginales univariadas, para obtener modelos más flexibles.
Esta Cópulas de distribuciones Elípticas, son llamadas en ocasiones Distribuciones Metaelípticas.
Cópula Normal o Gaussiana
La cópula Gaussiana o normal, Sea \((X,Y)\) una normal bivariada \((\Phi_2)\), con media nula, y \(\Sigma\) matriz de correlaciones.
\[ \Sigma= \begin{pmatrix} 1 & \rho \\ \rho & 1 \end{pmatrix} \]
Para cada componente cada componente es una normal estándar (\(\Phi\)). Al aplicar el Teorema de Sklar ( ver ejemplo) el resultado de la Cópula no es explícita, es decir a diferencia de las Cópulas arquimedianas que poseen una fórmula explícita, las Cópulas Elípticas no posee una forma explícita.
\[C(u,v)=\Phi_2(\Phi^{-1}(u),\Phi^{-1}(v))\]
\[=\frac{1}{2\pi\sqrt{1-\rho^2}}\int_{-\infty}^{\Phi^{-1}(u)}\int_{-\infty}^{\Phi^{-1}(v)}exp \left[\frac{-(s^2-2\rho st+t^2)}{2(1-\rho^2)}\right]dsdt\]
Para el caso bivariado, si \(\rho=-1\) es la contramonoticidad es decir la Cópula \(W\), para el caso \(\rho=0\) las variables son independientes y su Cópula seria \(\Pi\) y para el caso \(\rho=1\) la Cópula sería \(M\) (comonoticidad).
Otra Propiedad de la Cópula Normal es simétrica.
Cópula t-Student
Igualmente al ser una Cópula elíptica, tenemos una forma implícita de la Cópula, para el caso de sus variables (\(X,Y\)) y aplicando el Teorema de Sklar tenemos que:
\[C(u,v)=t_{2,\nu}(t^{-1}_\nu(u),t^{-1}_\nu(v))\] donde \(\nu\) son los grados de libertad y \(t_{2,\nu}\) es una t-student bidimensional con media nula y varianza \(\Sigma\) definidad anteriormente.
\[C(u,v)=\int_{-\infty}^{t_\nu^{-1}(u)}\int_{-\infty}^{t_\nu^{-1}(v)} \frac{K(\nu)}{\sqrt{1-\rho^2}}\left[1+\frac{s^2-2\rho st+t^2}{\nu(\sqrt{1-\rho^2})}\right]^{-\frac{\nu+2}{2}}[(1+\nu^{-1}s^2)(1+\nu^{-1}t^2)]^{\frac{\nu+2}{2}}dtds\]
Con \(K(\nu)=\Gamma(\nu/2)\Gamma((\nu+1)/2)^{-2}\Gamma(\nu/2+1)\)
A diferencia del caso de la Cópula Gaussiana, si \(\rho=0\) no se obtiene la Cópula \(\Pi\), es decir que ante la ausencia de la correlación, no implica independencia, el otro extremo \(\rho=1\) su Cópula es \(M\).
Cópulas de Valor Extremo
Esta cópulas son usadas para los casos de representar relaciones que eventos que ocurren en los extremos de las distribuciones marginales.
Supongamos que tenemos una m.a.s \((X,Y)=[(x_1,y_1),\dots,(x_n,y_n)]\) con distribución marginal \(F\) y \(G\) respectivamente y distribución conjunta \(H\) asociada a una Cópula \(C\). Consideremos el vector aleatorio de los máximos de cada variable dado por:
\[M_{(2)}=(M_1=max(x_1,...,x_n),M_2=max(y_1,...,y_n))\]
Cómo la muestras son independientes, la funciones marginales de \(M_{(2)}\) son \(F^{n}\),\(G^{n}\), por lo tanto la cópula asociada al vector aleatorio \(M_{(2)}\) esta dado por:
\[C_n(u,v)=C(u^{1/n},v^{1/n})^{n}\]
Esto por que
\[P(M_1\leq x,M_2 \leq y)=H(x,y)^n=C(F(x),G(y))^n=C((F(x)^n)^{1/n},(G(x)^n)^{1/n})^{1/n}\]
El grupo de la Cópulas de valor extremo surge cuando el límite las Cópulas \(C_n\) cuando \(n \to \infty\) existe.
Definición
Una Cópula \(C_{\infty}\) se dice de valor extremo si existe otra Cópula \(C\) tal que:
\[C(u^{1/n},v^{1/n})^{n} \to C(u,v), \quad n \to \infty\]