fnormal = function(x,mu1,mu2,varianza)
{
fx = exp( -((x - mu1)^2/(2*(varianza)))) +
exp( - ((x - mu2)^2/(2*(varianza))))
return(fx)
}7 Metropolis-Hastings
El objetivo de los métodos computacionales bayesianos se puede resumir en el cálculo de las Esperanzas Matemáticas.
Los procesos de Cadenas de Markov por MonteCarlo (MCMC), son una técnica que permite generar, de manera iterativa, observaciones de distribuciones, usualmente multivariadas que díficilmente podrían simularse con métodos directos.
La idea es la siguiente: Construir una cadena de Markov que sea fácil de simular y cuya distribución de equilibrio corresponda a la distribución que nos interesa.
Sea \(\theta^{(1)},\theta^{(2)}, cdots\) una cadena de Markov homogénea, irreductible y aperiódica, con espacio de estados \(\Theta\) y con distribución de equilibrio \(p(\theta | x)\). Enotnces, conforme \(t \rightarrow \infty\) se tiene que:
\[\theta^{(t)}\rightarrow \theta \sim p(\theta|x)\] Ejemplo
Consideremos un ejemplo para el caso discreto. Se tiene sólo dos posibilidades de estados \({0,1}\), con la siguiente matriz de transición \(P\)
\[ P= \begin{pmatrix} 0.2 & 0.8 \\ 0.1 & 0.9 \end{pmatrix} \] Resolviendo la ecuación \(\pi=\pi P\) se llega a la distribución de equilibrio donde
\[\pi=\left(\frac{1}{9},\frac{8}{9}\right)\]
Es decir, que para un tiempo grande, no importa en que estado inicie la cadena, la cadena tendrá la siguiente distribución estacionaria
\[P[X=0]=\frac{1}{9} \quad P[X=1]=\frac{8}{9}\] Es decir su distribución estacionara es una Bernoulli con parámetro 8/9.
7.1 Metropolis Hastings
El algoritmo de Metropolis surge del artículo de 1953 “Equation of State Calculations by Fast Computing Machines” escrito por Nicholas Metropolis, Arianna Rosenbluth, Marshall Rosenbulth, Augusta Teller y Edward Teller, que propuso el algoritmo para distribuciones simétricas. En 1970 Wilfred Hasting los generalizó en el artículo “Monte Carlo sampling methods using Markov chains and their apllications”
En particular el algoritmo de Métropolis-Hastings obtiene el estado de una cadena en el instante \(t+1\) muestreando un candidato \(Y\) de una distribución candidata \(q(\cdot |X_t)\). Esta distribución candidata sólo depende del estado previo \(X_t\) y debe cumplir algunas condiciones. Un ejemplo muy utilizado para \(q\) es la distribución normal multivariada con media \(X_t\) y matriz de covarianza \(\Sigma\) fija. Otras elecciones son posibles, pero un aspecto importante es que sean fáciles de muestrear.
Entre las condiciones de regularidad que se le imponen a \(q(\cdot|X_t)\) son:
Irreducibilidad: Existe una probabilidad positiva que la cadena alcance cualquier estado partiendo de cualquier estado inicial.
Aperiodicidad Es decir que la cadena no oscila entre diferentes conjuntos de estados.
El punto candidato \(Y\) es entonces aceptado como el siguiente de la cadena con probabilidad:
\[\alpha(X_t,Y) = min \left\{1,\frac{\pi(Y)q(Y|X_t)}{\pi(X_t)q(X_t|Y)}\right\}\]
Si el punto \(Y\) no es aceptado, entonces la cadena permanece en \(X_t\), en el caso del muestreo de una densidad a posteriori \(\pi(\theta|x) \propto \pi(\theta)L(x|\theta)\) conocida la densidad condicional \(q(\theta^*|\theta)\) fácil de muestrear,
El algoritmo de Metrópolis-Hastings consiste en:
Algoritmo Metropolis-Hasting
- Asiginar un valor inicial \(\theta^{(0)}\),
- t=0
- generar \(\theta \sim q(\theta|\theta^{(t)})\)
- Definir:
\[\alpha(\theta^{(t)},\theta) = min \left\{1,\frac{L(x|\theta)q(\theta^{(t)}|\theta)}{L(x|\theta^{(t)})q(\theta|\theta^{(t)})}\right\}\]
Hacer \(\theta^{(t+1)}=\theta\) con probabilidad \(\alpha(\theta^{(t)},\theta)\) ó \(\theta^{t+1}=\theta^{t}\) en caso contrario.
t=t+1 regresar al paso 3.
Algunos comentarios respecto al algoritmo:
- En el caso particular que \(q\) sea simétrica es decir que \(q(X|Y)=q(Y|X)\) entonces estamos en el método original propuesto por Metrópolis et al (1953)
\[\alpha(X_t,Y) = min \left\{ 1,\frac{\pi(Y)}{\pi(X_t)}\right\}\]
Para analizar la convergencia de este algoritmo se pueden realizar diagnósticos formales , aunque en la práctica se toman distintos valores iniciales, análisis gráfico y medias estimadas (promedio ergódico), suelen ser un buen test inicial para asegurar la convergencia del algoritmo.
Los primeros valores de la cadena resultante suelen estar muy correlacionados, a diferencia del algoritmo de Aceptación-Rechazo que genera muestras independientes, dada esta correlación puede que los primeros estados de la cadena tenga una distribución diferente a la deseada, por lo que se desechan las primeras observaciones (usualmente las primeras 1000) para el análisis inferencial, a esto se le llama burn-in o quemado.
Métodos como el de Aceptación-Rechazo poseen la “Maldición dimensional” donde la probabilidad de rechazo aumenta exponencialmente en función de las variables. El Método de Metropolis-Hasting junto con otros procesos de Monte Carlo no tiene este problema, por lo que son la opción preferible cuando el número de variables de la distribución es alto.
7.2 Ejemplo 1
Utilizaremos el algoritmo de Metropolis-Hasting para conocer la distribución del resultado de la suma de dos normales con diferente medias \((\mu_1,\mu_2)\) con igual varianza \((\sigma^2)\), una situación que es díficil de calcularla, por lo que construiremos el núcleo de la distribución \(\pi(x)\).
En este caso el núcleo de la distribución sería
\[f(x)= e^{-\frac{1}{2}\frac{(x-\mu1)^2}{\sigma^2}}+e^{-\frac{1}{2}\frac{(x-\mu2)^2}{\sigma^2}}\]
y la constante de normalización sería:
\[K=\frac{1}{2\sqrt{2\pi\sigma^2}}\]
Algunos ejemplos con diferentes parámetros para \(\mu_1,\mu_2,\sigma^2\)
par(mfrow=c(2,2))
curve(fnormal(x,12,5,4), from=-16,to=16, type="l",main="Distribucion(x) para (12,10)",xlab="x",ylab="f(x)")
curve(fnormal(x,-8,8,4),from=-16,to=16,type="l",main="Distribucion(x) para (-8,8)",xlab="x",ylab="f(x)")
curve(fnormal(x,0,3,2),from=-16,to=16, type="l",main="Distribucion(x) para (0,3)",xlab="x",ylab="f(x)")
curve(fnormal(x,6,3,1),from=-16,to=16, type="l",main="Distribucion(x) para (6,3)",xlab="x",ylab="f(x)")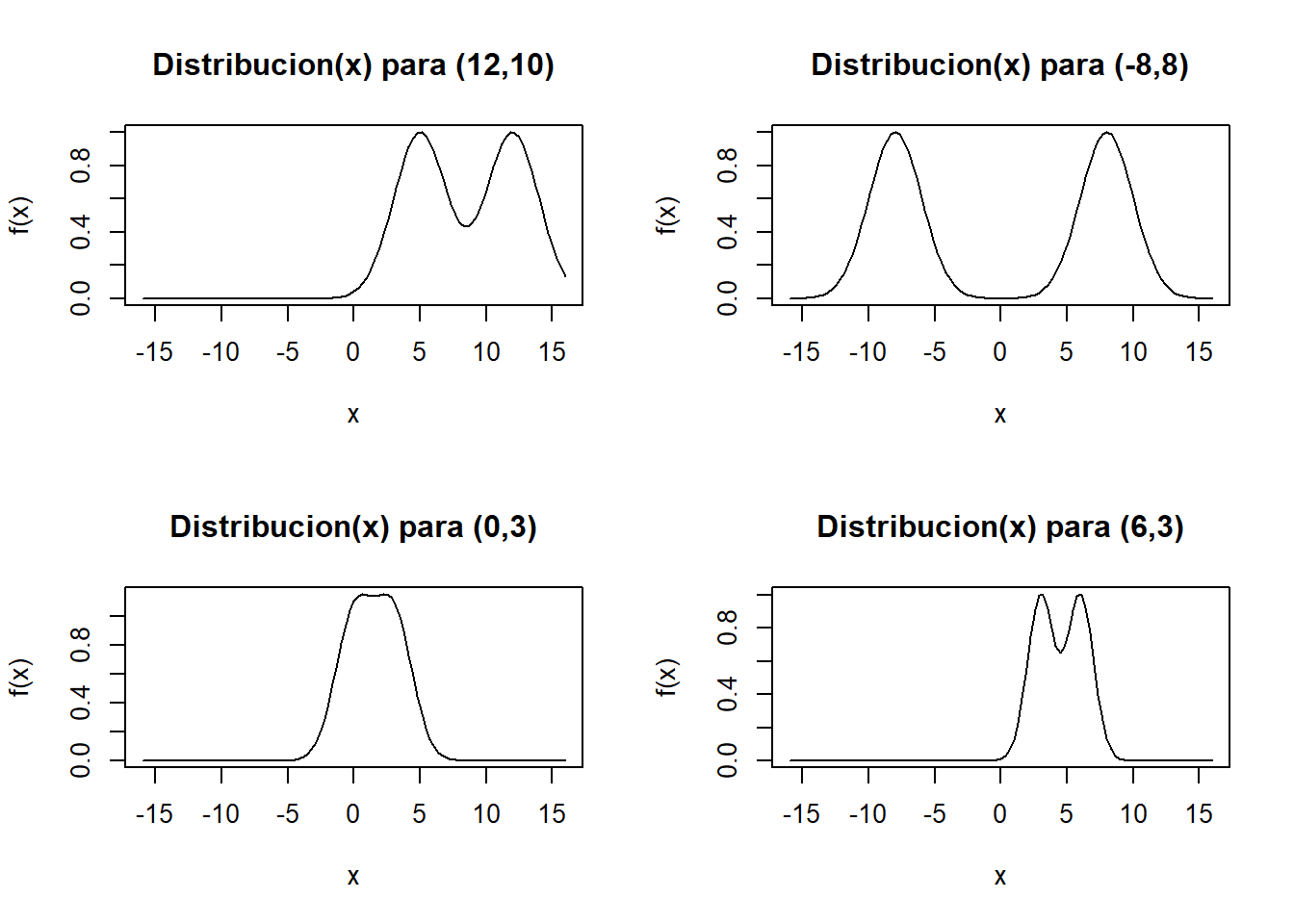
par(mfrow=c(1,1))Para este ejemplo usaremos obtendremos la muestra de la distribución \(\pi(x)\) para \(\mu_1 = 8,\mu_2 = 4, \sigma^2=1\)
mu1 = 8
mu2 = 4
sigma = 1
fPI = function(x){return(fnormal(x,mu1,mu2,sigma))}
curve(fPI(x), from=0,to=16, type="l",main="Distribucion(x) aprox N(8,1) + N(4,1)",xlab="x",ylab="f(x)")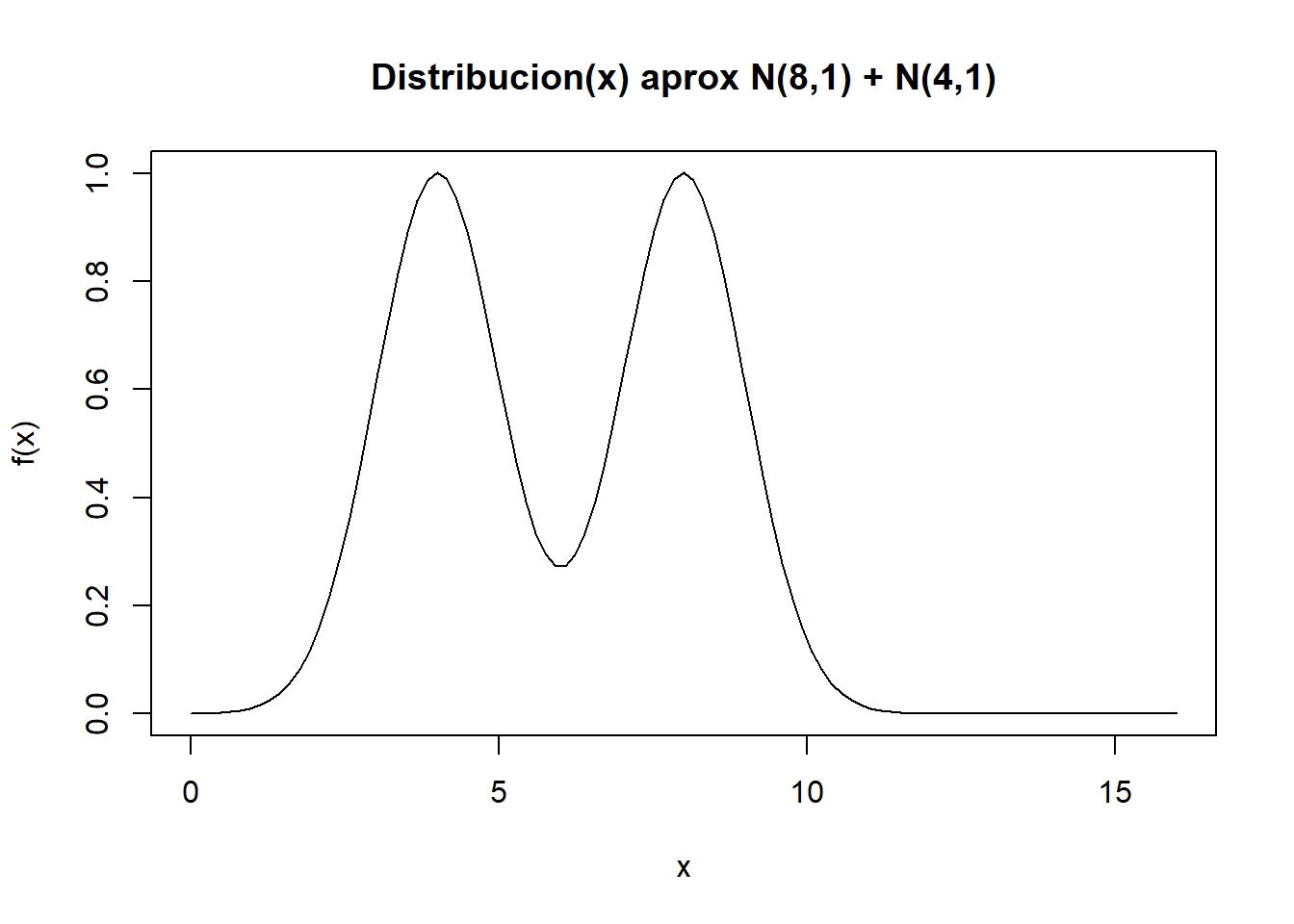
Para aplicar el algoritmo de Metropolis-Hasting es necesario contar con una función \(q(\cdot|Y)\) que será la Cadena a Markov a utilizar que nos permitirá encontrar la distribución a posteriori, que tiene como distribución estacionaria la función \(\pi(x)=f(x)\)
Para efectos del ejemplo usaremos una función de distribución de Cauchy
fpK = function(x,y){
pK = dcauchy(y,location = x) #x es el centro del pico de la distribución.
return(pK)
}
par(mfrow=c(1,1))Algunos ejemplos que toma \(q(\cdot|Y)\)
fpK = function(x,y){
pK = dcauchy(y,location = x) #x es el centro del pico de la distribución.
return(pK)
}
par(mfrow=c(2,2))
y=seq(-10,10,0.01)
x = 5
plot(y,fpK(x,y), type="l",main="Densidad de K(5,y)",xlab="y",ylab="K(5,y)")
x = -1
plot(y,fpK(x,y), type="l",main="Densidad de K(-1,y)",xlab="y",ylab="K(-1,y)")
x=seq(-10,10,0.01)
y = 3
plot(x,fpK(x,y), type="l",main="Densidad de K(x,3)",xlab="x",ylab="K(x,3)")
y = -5
plot(x,fpK(x,y), type="l",main="Densidad de K(x,-5)",xlab="x",ylab="K(x,-5)")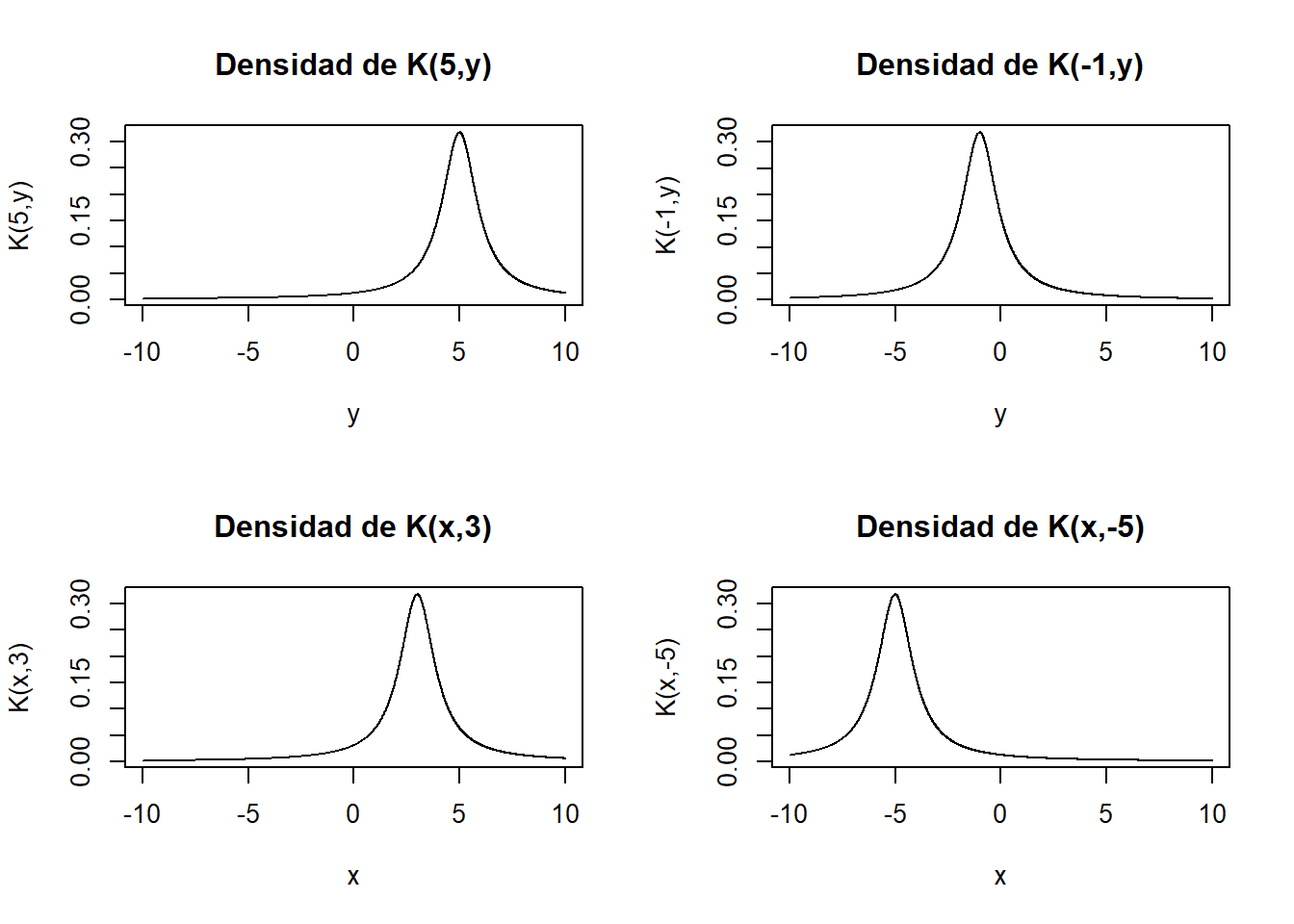
Con los gráficos, podemos verificar visualmente que \(q(\cdot|Y)\) tiene el mismo dominio que la distribución \(\pi(x)\) y que en particular es siempre positiva (al ser una distribución).
Procederemos con el algoritmo:
N = 10^5 # Número de Iteraciones
L = 1000 # periodo quemado (burn in)
MCMC = matrix(data = 0, nrow = N, ncol = 12)
colnames(MCMC) =
c("x","y","PIx","PIy","Kxy","Kyx","Rxy","Ryx","Mxy","Myx","Fxy","Salto")
# 1. Inicial con un valor arbitrario de x del dominio de distribución
x = runif(1,-50,50)
for (i in 1:N){
# 2. Generamos la propuesta con una distribucion arbitraria
y = rcauchy(1,location = x) #Valor aleatorio según X
#3. Tasa de Aceptación
PIx = fPI(x)
PIy = fPI(y)
Kxy = fpK(x,y)
Kyx = fpK(y,x)
Rxy = (PIy*Kyx) / (PIx*Kxy)
Ryx = (PIx*Kxy) / (PIy*Kyx)
# Matriz estocástica de los estados de la distribución estacionaria
if(x!=y){Mxy = Kxy*min(1,Rxy)
Myx = Kyx*min(1,Ryx)}
else{ Mxy = -1
Myx = -1}
#4. Criterio de Aceptacion o Rechazo
#Probabilidad de aceptación,runif(1)
Fxy = runif(1)
MCMC[i,] = c(x,y,PIx,PIy,Kxy,Kyx,Rxy,Ryx,Mxy,Myx,Fxy,0)
if (is.na(Rxy)) {Rxy = 0} else if (!is.finite(Rxy)) {Rxy = 1}
#Control sobre Rxy, si da valores muy pequeño, R pone NA o si muy grandes puede dar infinito.
if(Fxy < Rxy){
x = y
lsalto = 1}
else{lsalto = 0}
MCMC[i,12] = lsalto
}
mcmc = MCMC[(L+1):N,"x"]
head(mcmc,50) [1] 6.449918 6.449918 7.414950 7.414950 7.986233 7.123122 7.828537 7.287332
[9] 7.287332 8.397964 8.397964 8.397964 6.750197 7.073289 7.073289 8.491980
[17] 8.491980 7.760176 7.760176 7.760176 6.876650 7.327706 7.525571 5.176962
[25] 5.599790 5.599790 5.599790 4.133168 3.886445 3.886445 3.886445 3.797162
[33] 4.218021 4.663736 4.663736 4.755343 4.755343 5.072864 5.072864 3.735841
[41] 3.606498 3.606498 3.190922 3.738243 4.935516 4.889486 4.411181 4.977706
[49] 7.173296 7.209866Compararemos la muestra obtenida.
par(mfrow=c(2,2))
media=mean(mcmc)
curve(fPI(x), from=0,to=16, type="l",main="distribucion(x) aprox N(8,1) + N(4,1)",xlab="x",ylab="distribucion(x)")
abline(v=mu1, col='blue', lwd=3)
abline(v=mu2, col='red', lwd=3)
abline(v=media, col='violet', lwd=3)
hist(mcmc,
freq = FALSE,
main = "Distribucion de muestra MCMC",
xlab = "x",
ylab = "distribucion(x)",
breaks = 200)
abline(v=mu1, col='blue', lwd=3)
abline(v=mu2, col='red', lwd=3)
abline(v=media, col='violet', lwd=3)
#Traceplot
plot(mcmc,type="l",xlab = "x", ylab = "y", main = "Traceplot de muestra MCMC")
abline(h=mu1, col='blue', lwd=3)
abline(h=mu2, col='red', lwd=3)
abline(h=media, col='violet', lwd=3)
#Grafico de Autocorrelación
acf(mcmc,main = "Autocorrelacion de muestra MCMC")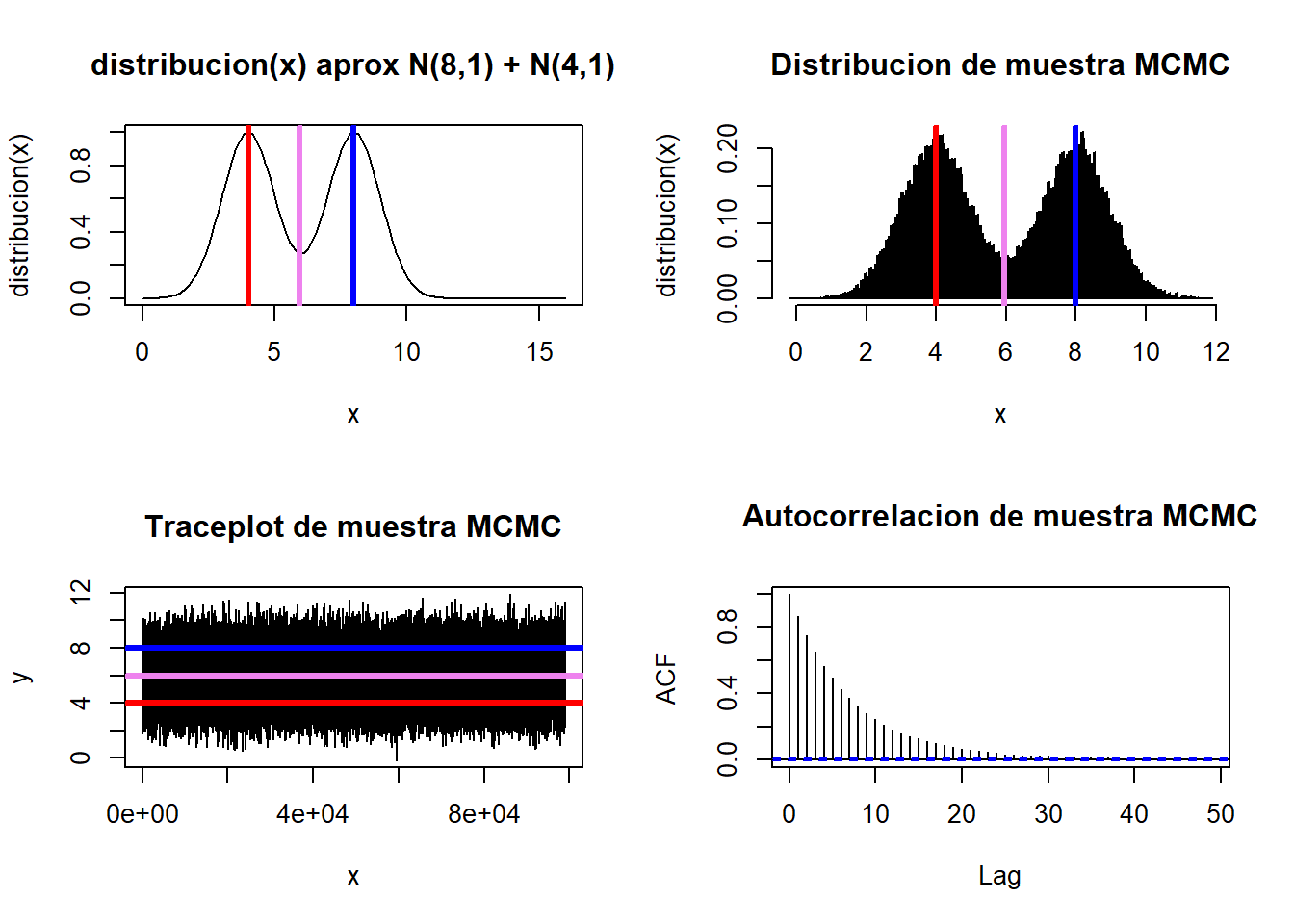
par(mfrow=c(1,1))
#Grafico convergencia de la media (Promedio ergodico)
m=N-L
acumulado<-cumsum(mcmc)/(1:m)
plot(1:m,acumulado,col="blue",type="l",ylab="promedio",xlab="Iteraciones") 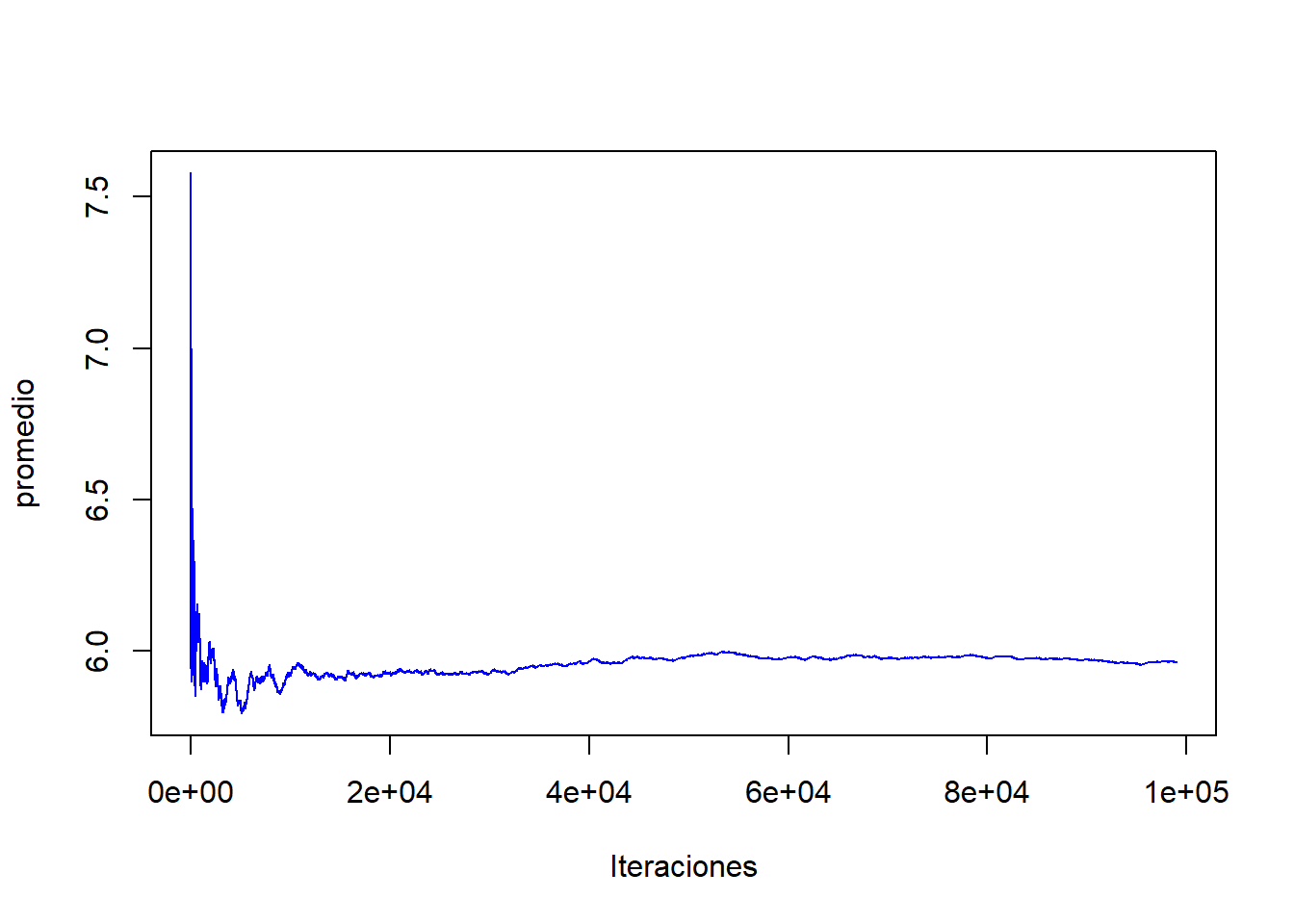
mean(mcmc)[1] 5.961192cat("Tasa de aceptación \n",
"NumeroSaltos/TotalIteraciones :" , mean(MCMC[,"Salto"]) ,"\n") Tasa de aceptación
NumeroSaltos/TotalIteraciones : 0.62508 Balance Detallado
Muchas probabiliddes de transición satisfacen la propiedad de balance detallado:
\[\pi(x)q(x|y)=\pi(y)q(y|x)\]
Esta ecuación dice que si tomamos un estado inicial de la densidad objetivo \(q(\cdot|\cdot)\) y la hacemos una transición según \(M(x,y)\) hasta otro estado, es igualmente probable tomar \(x\) e ir hasta \(y\), que tomar \(y\) e ir hasta \(x\).
Las Cadenas de Markov que satisfacen el balance detallado, se denominan Cadenas de Markov Reversibles.
La razón por la cual la propiedad del balance detallado es interesante es que implica la invarianza de la distribución bajo la cadena de Markov, es una distribución estacionaria, que es una condición necesaria para la propiedad que queremos de nuestra simulación MCMC.
El Algoritmo de Metropolis-Hasting satisface el balance detallado. Sin embargo, el balance detallado no es una condición esencial, ya que se puede trabajar con Cadenas irreversibles según sus propiedades, como son las caminatas aleatorias.
Verifiquemos el Balance Detallado del Ejemplo Anterior
dfMCMC = as.data.frame(MCMC[(L+1):N,c("PIx","PIy","Mxy","Myx","Salto")])
head(dfMCMC) PIx PIy Mxy Myx Salto
1 0.3505146 0.2965103 0.1801508 0.21296222 0
2 0.3505146 0.8456373 0.1648176 0.06831649 1
3 0.8456373 0.6774151 0.0347175 0.04333888 0
4 0.8456373 1.0002597 0.2399866 0.20288896 1
5 1.0002597 0.6884400 0.1255503 0.18241657 1
6 0.6884400 0.9860641 0.2125451 0.14839253 1dfMCMC$Balance = dfMCMC$PIx*dfMCMC$Mxy - dfMCMC$PIy*dfMCMC$Myx
par(mfrow=c(2,1))
hist(dfMCMC$Balance,
prob = FALSE,
main = "Distribucion Balanceo Detallado",
xlab = "x",
ylab = "Distribucion(x)",
breaks = 300)
plot( dfMCMC$Balance,type="l",xlab = "x", ylab = "y",
main = "Distribucion Balanceo Detallado")
abline(h=0.00, col='red', lwd=3)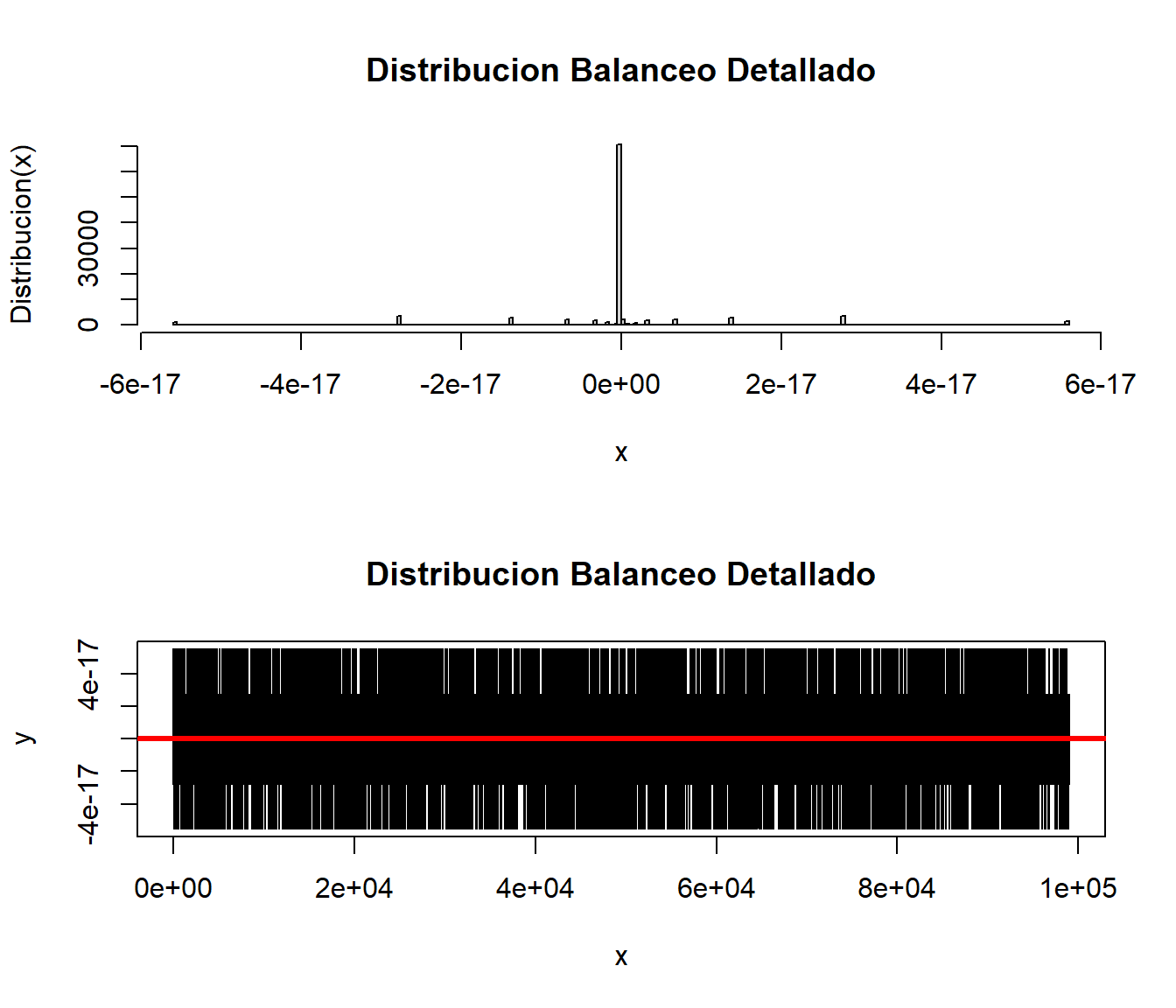
par(mfrow=c(1,1))Como se puede observar las diferencias se concentran alrededor del 0, y en el Traceplot se observa esa tendencia.
Si obtenemos la media y la varianza de los valores obtenidos en la diferencia son nulos, podemos afirmar que se cumple la condición de Balance detallado, redondearemos a 15 decimales.
cat("Distribucion Balanceo Detallado\n",
"Media :" ,round(mean(dfMCMC$Balance), 15),"\n",
"Varianza:" ,round(var(dfMCMC$Balance) ,15))Distribucion Balanceo Detallado
Media : 0
Varianza: 07.3 Ejemplo 2
Tomaremos una muestra de \(x_1,x_2,....x_n\) con \(x_i \sim \gamma(\alpha, \beta)\) en particular tomaremos \(\alpha=2, \beta=1\), para estimar usando el algoritmo de Metropolis-Hasting el valor de \(\alpha\)
n <- 100
nsim <- 10^4 #numero de simulaciones
set.seed(54321)
mx <- rgamma(n,2,1)
lik <- Vectorize(function(x) prod(dgamma(mx,x,1)))
curve(dgamma(x,2,1),from=0,to=10)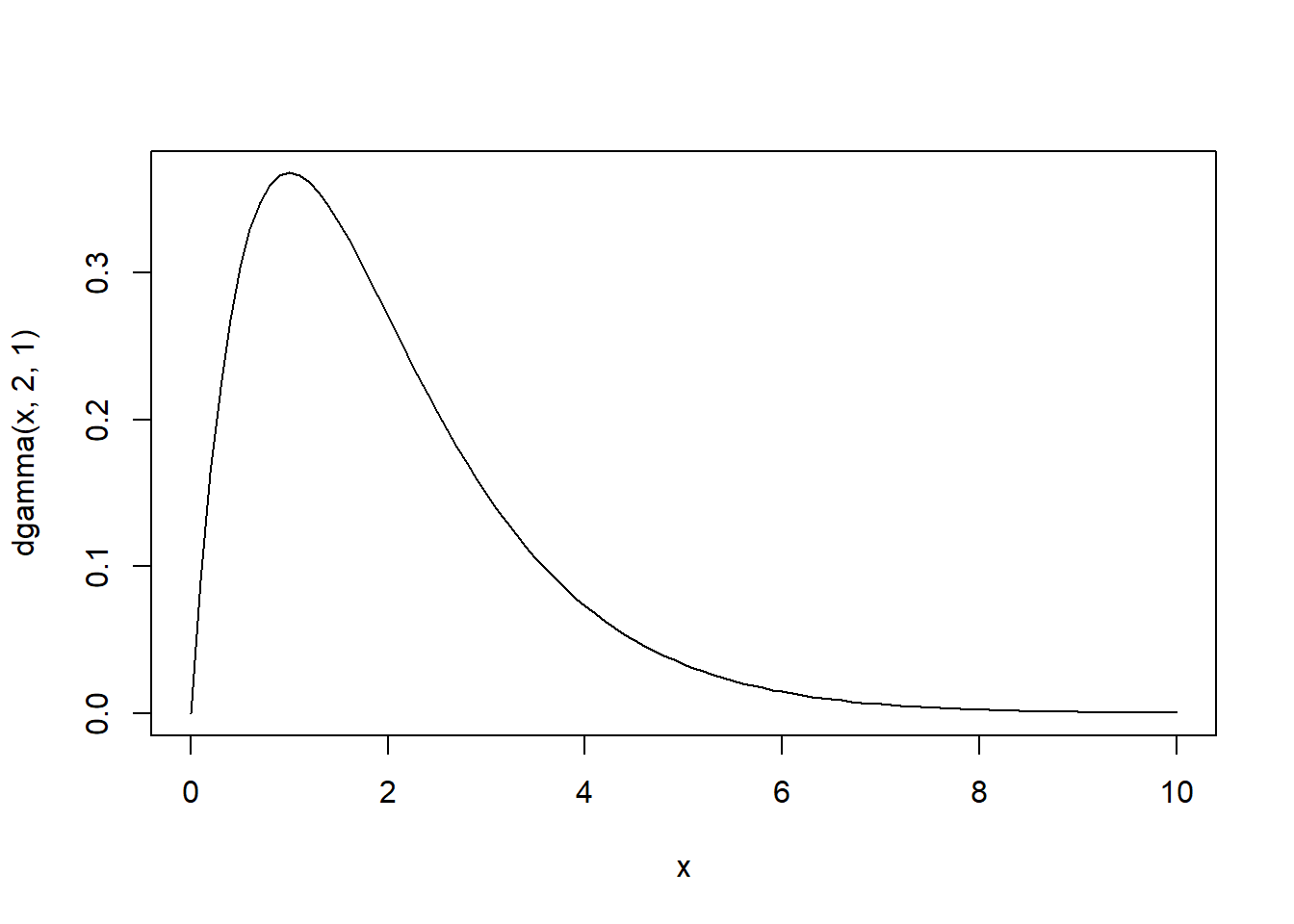
Usaremos como función \(q(\cdot|\cdot)\) una función exponencial con parámetro = 1.
L = 1000 # periodo quemado (burn in)
MCMC = matrix(data = 0, nrow = N, ncol = 5)
colnames(MCMC) =
c("x","PIx","PIy","Fxy","Salto")
x = runif(1,0,100)
for (i in 1:nsim){
# 2. Generamos la propuesta con una distribucion arbitraria
y = rexp(1,1) #Valor aleatorio según X
PIx = lik(x)
PIy = lik(y)
Kxy = dexp(x,1)
Kyx = dexp(y,1)
(Rxy = (PIy*Kyx) / (PIx*Kxy))
(Fxy = runif(1))
MCMC[i,] = c(x,PIx,PIy,Fxy,0)
if(Fxy < Rxy){
x = y
lsalto = 1}
else{lsalto = 0}
MCMC[i,5] = lsalto
}
mcmc = MCMC[(L+1):nsim,"x"]
head(mcmc,50) [1] 2.046830 2.046830 2.046830 2.046830 2.046830 1.989972 1.989972 1.989972
[9] 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972
[17] 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972
[25] 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972
[33] 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972
[41] 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972 1.989972
[49] 1.989972 1.989972Compararemos la muestra obtenida.
par(mfrow=c(2,2))
media=mean(mcmc)
curve(lik(x), from=1,to=3, type="l")
abline(v=media, col='violet', lwd=3)
hist(mcmc,
freq = FALSE,
main = "Distribucion de muestra MCMC",
xlab = "x",
ylab = "distirbucion(x)",
breaks = 200)
abline(v=media, col='violet', lwd=3)
#Traceplot
plot(mcmc,type="l",xlab = "x", ylab = "y", main = "Traceplot de muestra MCMC")
abline(h=media, col='violet', lwd=3)
#Grafico de Autocorrelacion
acf(mcmc,main = "Autocorrelacion de muestra MCMC")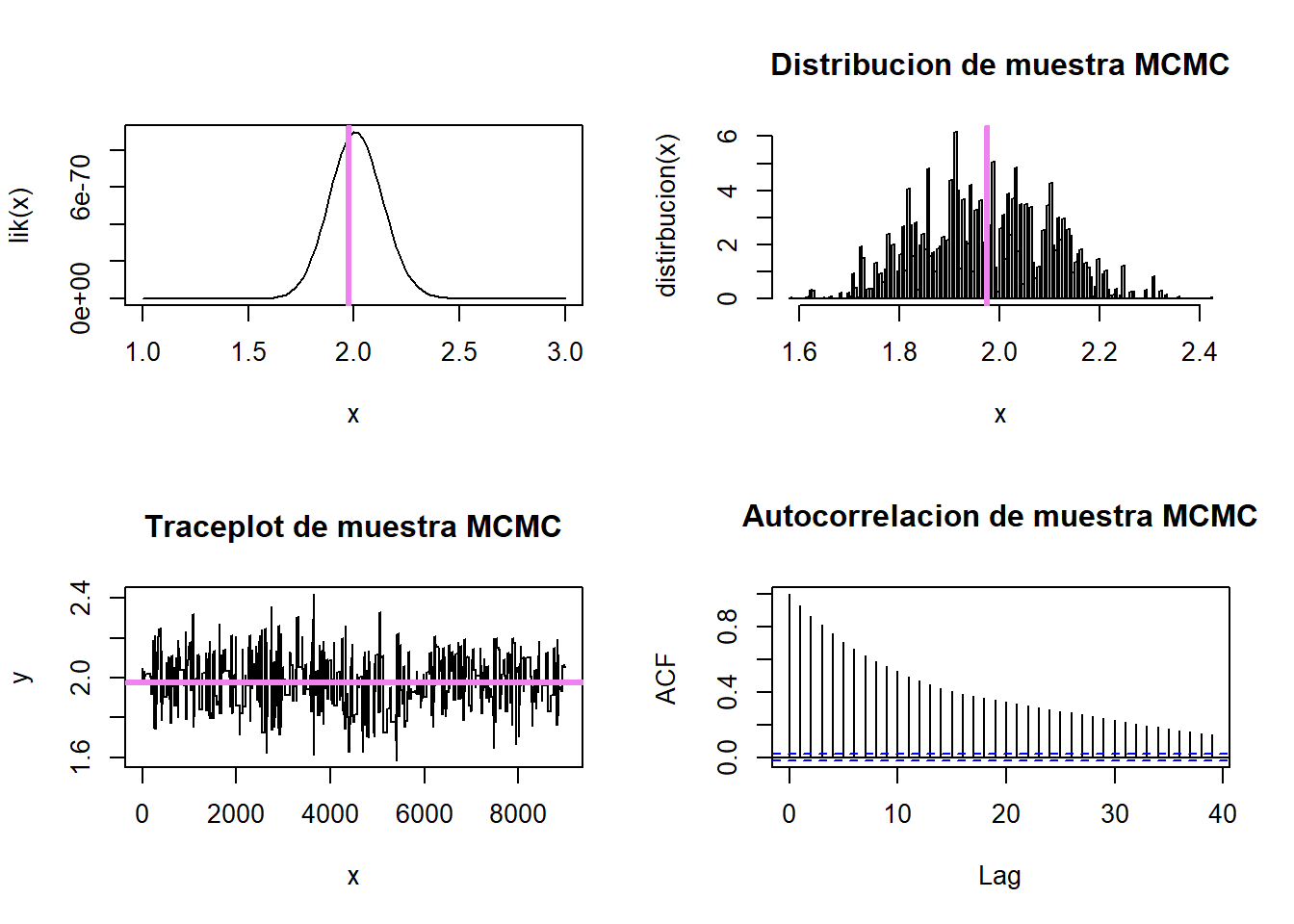
par(mfrow=c(1,1))
#Grafico convergencia de la media
m=nsim-L
acumulado<-cumsum(mcmc)/(1:m)
plot(1:m,acumulado,col="blue",type="l",ylab="promedio",xlab="Iteraciones") 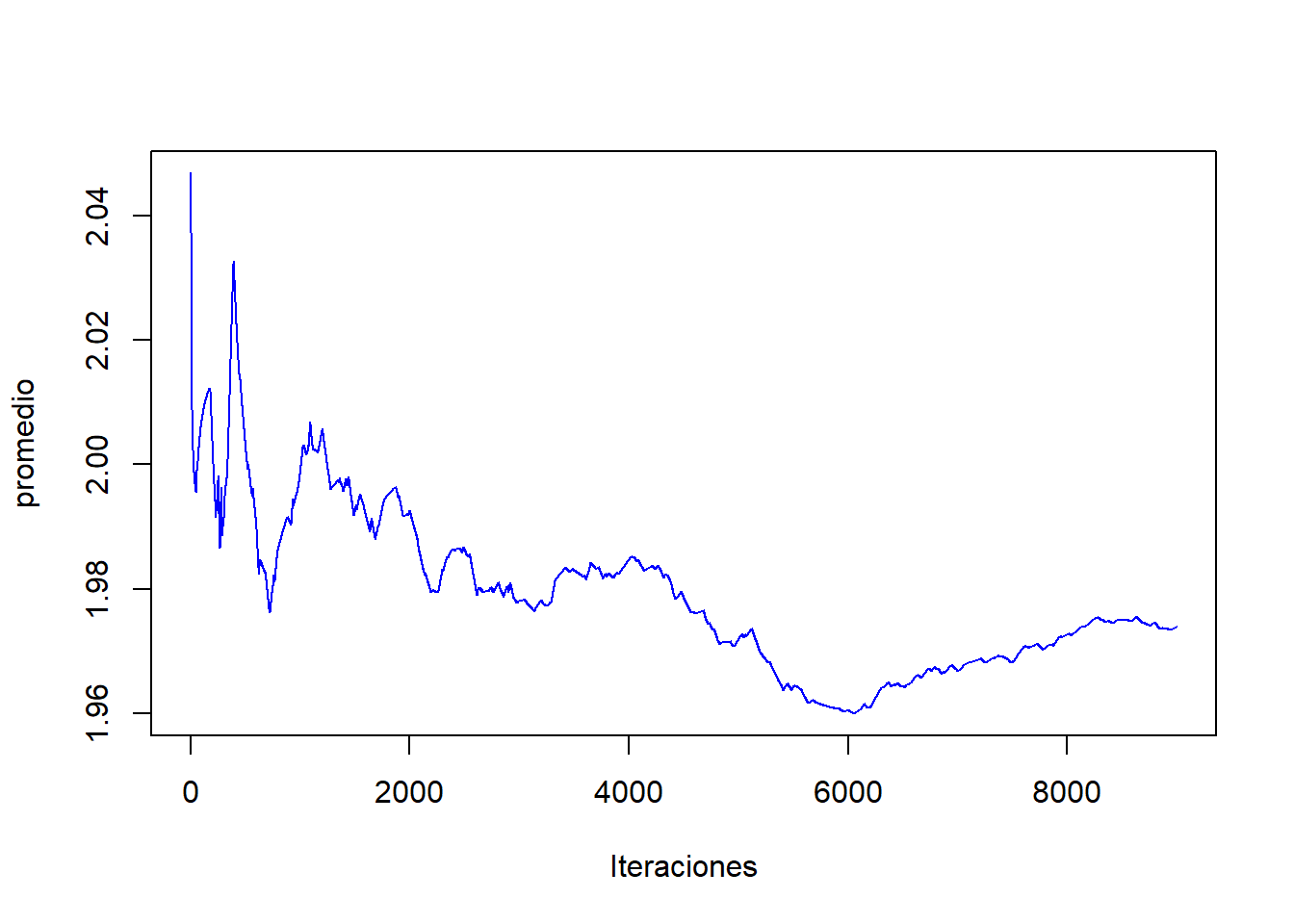
media[1] 1.973907cat("Tasa de aceptacion \n",
"NumeroSaltos/TotalIteraciones :" , mean(MCMC[,"Salto"]) ,"\n") Tasa de aceptacion
NumeroSaltos/TotalIteraciones : 0.00527 Como se puede observar el algoritmo converge, pero muy lentamente, posee mucha autocorrelación, aunque el valor a estimar es cercano. En estos casos tenemos las siguientes opciones:
Aumentar la iteraciones para disminuir la autocorrelación
Cambiar la distribución.
Una combinación de ambas.
Para mejorar nuestro modelo, cambiaremos el parametro \(\lambda\) de la distribución exponencial, que es nuestra función \(q(\cdot|\cdot)\)
nsim=10^5
L = 1000 # periodo quemado (burn in)
MCMC = matrix(data = 0, nrow = N, ncol = 5)
colnames(MCMC) =
c("x","PIx","PIy","Fxy","Salto")
x = runif(1,0,100)
for (i in 1:nsim){
# 2. Generamos la propuesta con una distribucion arbitraria
y = rexp(1,0.5) #Valor aleatorio según X
PIx = lik(x)
PIy = lik(y)
Kxy = dexp(x,0.5)
Kyx = dexp(y,0.5)
(Rxy = (PIy*Kyx) / (PIx*Kxy))
#Criterio de Aceptacion o Rechazo
#Probabilidad de aceptación,runif(1)
(Fxy = runif(1))
MCMC[i,] = c(x,PIx,PIy,Fxy,0)
if(Fxy < Rxy){
x = y
lsalto = 1}
else{lsalto = 0}
MCMC[i,5] = lsalto
}
mcmc = MCMC[(L+1):nsim,"x"]
head(mcmc,50) [1] 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125
[9] 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125
[17] 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125
[25] 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125 1.958125
[33] 1.957551 1.957551 1.957551 1.957551 1.957551 1.957551 1.957551 1.957551
[41] 1.957551 1.957551 1.957551 1.957551 1.957551 1.957551 1.957551 1.957551
[49] 1.957551 1.957551Compararemos la muestra obtenida.
par(mfrow=c(2,2))
media=mean(mcmc)
curve(lik(x), from=1,to=3, type="l")
abline(v=media, col='violet', lwd=3)
hist(mcmc,
freq = FALSE,
main = "Distribucion de muestra MCMC",
xlab = "x",
ylab = "distribucion(x)",
breaks = 200)
abline(v=media, col='violet', lwd=3)
#Traceplot
plot(mcmc,type="l",xlab = "x", ylab = "y", main = "Traceplot de muestra MCMC")
abline(h=media, col='violet', lwd=3)
#Grafico de Autocorrelación
acf(mcmc,main = "Autocorrelacion de muestra MCMC")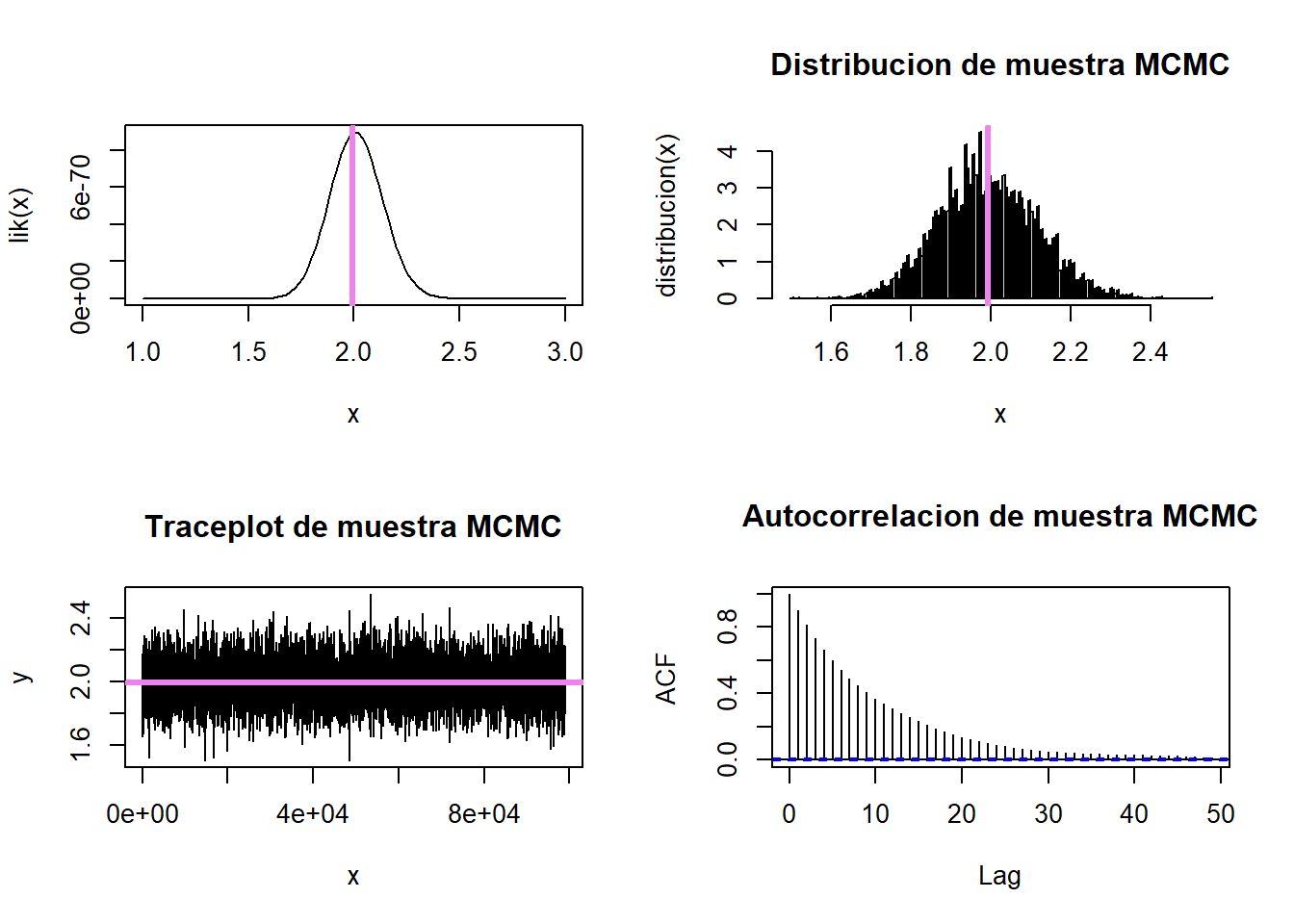
par(mfrow=c(1,1))
#Grafico convergencia de la media
m=nsim-L
acumulado<-cumsum(mcmc)/(1:m)
plot(1:m,acumulado,col="blue",type="l",ylab="promedio",xlab="Iteraciones") 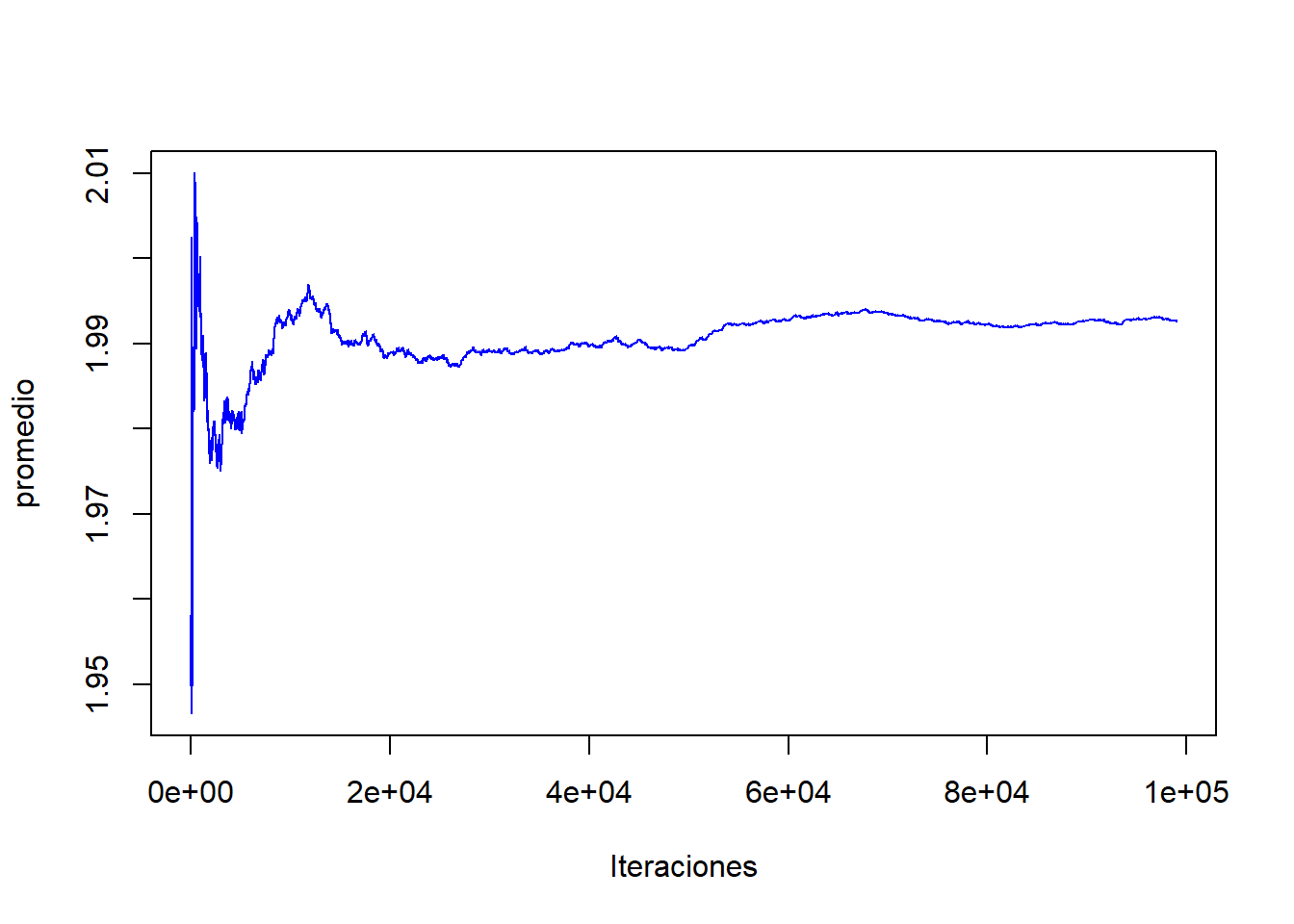
media[1] 1.992614cat("Tasa de aceptacion \n",
"NumeroSaltos/TotalIteraciones :" , mean(MCMC[,"Salto"]) ,"\n") Tasa de aceptacion
NumeroSaltos/TotalIteraciones : 0.07386 8 Muestreo de Gibbs
El muestreo de Gibbs es un algoritmo que nos permite generar una muestra aleatoria dada una distribución conjunta de dos o más variables aleatorias. A diferencia de los algoritmos anteriores, este el algoritmo es sólo válido en los casos de dos o más variables, aunque los anteriores se pueden extender a más dimensiones, el algortimo de Gibbs siempre se usa para dos o más variables.
El algoritmo los exponen dos hermanos (Stuart y Donald) Geman en 1984, 80 años después de la muerte de Willard Gibbs, dado sus trabajos en física estadística.
El muestreo de Gibbs también lo llaman muestreo condicional alterno es una generalización del modelo de Metropolis, es fácil de implementar pero no tan eficiente para una simulación directa de la distribución.
Para implementar el muestreo de Gibbs se necesita ser capaz de generar muestras de la distribución a posteriori condicional a cada uno de los parámetros individuales. Esto es, que el algortimo permite generar muestras de:
\[p(\theta_1,\theta_2,... \theta_n|x)\]
siempre y cuando podamos generar valores de todas las distribuciones condicionales, es decir
\[p(\theta_k|\theta_1,...\theta_{k-1},\theta_{k+1},...\theta_{n},x)\]
El proceso de muestras de Gibbs es una caminata aleatoria a lo largo del espacio de los parámetros. La caminata inicia en un punto arbitrario y en cada tiempo el siguiente paso depende únicamente de la posición actual (Markov).
El Algoritmo
Dar los valores inciales \(\theta^{(0)}=(\theta_1^{(0)},...,\theta_n^{(0)})\)
t=0
generar \(\theta_k^{(t+1)}=(\theta_1^{(t)},...,\theta_{k-1}^{(t)},\theta_{k+1}^{(t)},...,\theta_n^{(t)})\)
t=t+1
ir a 3
Este algoritmo es útil cuando no podemos determinar de manera analítica la distribución conjunta y no se puede simular directamente de ella, pero si podemos determinar todas las distribuciones condicionales y muestrarlas.
8.1 Ejemplo 1
Consideremos dos variables independientes \(\mu, \sigma^2\). una m.a.s. \(y=(y_1,...y_n)\) bajo un modelo Normal es decir que:
\[y_i|\mu, \sigma^2 \sim N(\mu, \sigma^2) \;i=1,...,n\]
Con distribuciones a priori
\[\mu \sim N(\mu_0, \tau_0^2)\]
\[\sigma^2 \sim GI(\upsilon_0/2,\upsilon_0\sigma_0^2/2)\]
(Resolver ejercicio)
# datos
y <- c(1.64,1.70,1.72,1.74,1.82,1.82,1.82,1.90,2.08)
# tamaño de la muestra
n <- length(y)
# estadisticos
(mean.y <- mean(y))[1] 1.804444(var.y <- var(y))[1] 0.01687778(sum.y <- sum(y))[1] 16.24Aplicando el Algortimo
# hiperparametros
mu0 <- 1.9
t20 <- 0.5^2
s20 <- 0.01
nu0 <- 1
# numero de muestras
S <- 100000
# matriz para almacenar las muestras
PHI <- matrix(data = NA, nrow = S, ncol = 2)
# mostrar cada 10% de las iteraciones
ncat <- floor(S/10)
# ALGORITMO (muestreador de Gibbs)
# 1. inicializar la cadena
set.seed(2024)
phi <- c( rnorm(1, mu0, sqrt(t20)), rgamma(1, nu0/2, nu0*s20/2) )
PHI[1,] <- phi
# 2. simular iterativamente de las distribuciones condicionales completas
set.seed(1478539)
for(s in 2:S) {
# 2.1 actualizar el valor de theta
t2n <- 1/( 1/t20 + n*phi[2] )
mun <- (mu0/t20 + sum.y*phi[2]) * t2n
phi[1] <- rnorm( 1, mun, sqrt(t2n) )
# 2.2 actualizar el valor de sigma^2
nun <- nu0+n
s2n <- (nu0*s20 + (n-1)*var.y + n*(mean.y-phi[1])^2)/nun
phi[2] <- rgamma(1, nun/2, nun*s2n/2)
# 2.3 almacenar
PHI[s,] <- phi
# 2.4 progreso
if(s%%ncat == 0) cat(100*round(s/S, 1), "% completado ... \n", sep = "")
}10% completado ...
20% completado ...
30% completado ...
40% completado ...
50% completado ...
60% completado ...
70% completado ...
80% completado ...
90% completado ...
100% completado ... Podemos graficar los pasos del algortimo, no es usual en la práctica realizar este gráfico
par(mfrow=c(1,3),mar=c(2.75,3,.5,.5),mgp=c(1.70,.70,0))
m1<-5
plot(PHI[1:m1,],type="l",xlim=range(PHI[1:100,1]), ylim=range(PHI[1:100,2]),
lty=1,col="gray",xlab=expression(theta),ylab=expression(tilde(sigma)^2))
text(PHI[1:m1,1], PHI[1:m1,2], c(1:m1) )
m1<-15
plot(PHI[1:m1,],type="l",xlim=range(PHI[1:100,1]), ylim=range(PHI[1:100,2]),
lty=1,col="gray",xlab=expression(theta),ylab=expression(tilde(sigma)^2))
text(PHI[1:m1,1], PHI[1:m1,2], c(1:m1) )
m1<-100
plot(PHI[1:m1,],type="l",xlim=range(PHI[1:100,1]), ylim=range(PHI[1:100,2]),
lty=1,col="gray",xlab=expression(theta),ylab=expression(tilde(sigma)^2))
text(PHI[1:m1,1], PHI[1:m1,2], c(1:m1) )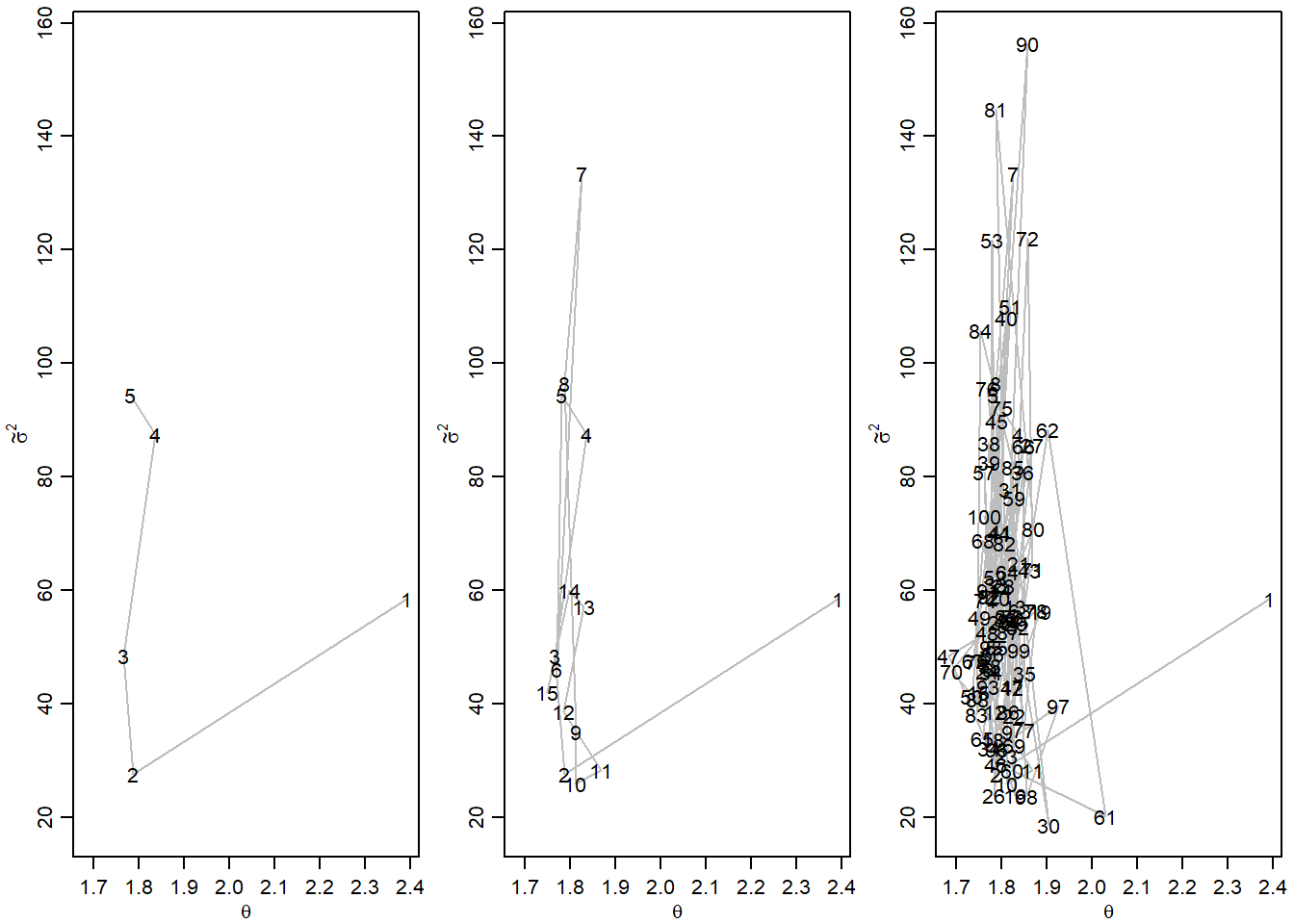
Graficaremos el Traceplot
LL <- NULL
for (i in 1:S)
LL[i] <- sum(dnorm(x = y, mean = PHI[i,1], sd = sqrt(1/PHI[i,2]), log = T))
# graficos
par(mfrow=c(3,1), mar=c(3,3,1,1), mgp=c(1.75,.75,0))
# traceplots
plot(PHI[,1], type = "l", xlab="iteration", ylab=expression(theta))
abline(h = mean(PHI[,1]), col = 4, lty = 2, lwd = 2)
plot(1/PHI[,2], type = "l", xlab="iteration", ylab=expression(sigma^2))
abline(h = mean(1/PHI[,2]), col = 4, lty = 2, lwd = 2)
plot(LL, type = "l", xlab="iteration", ylab="lLog-verosimilitud")
abline(h = mean(LL), col = 4, lty = 2, lwd = 2)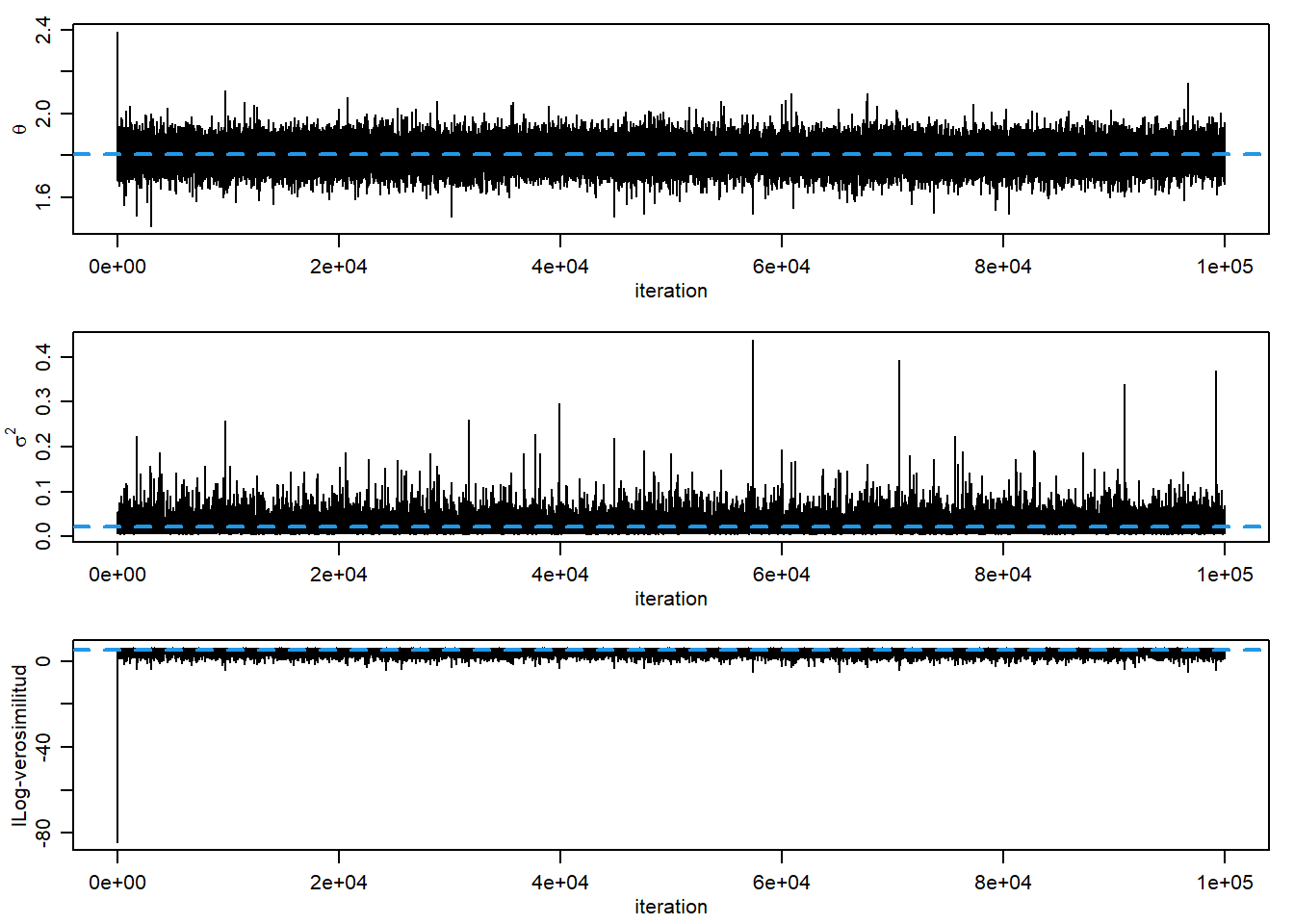
Graficaremos la autocorrelación
par(mfrow = c(1,2), mar=c(3,3,3,1), mgp=c(1.75,.75,0))
acf(PHI[,1], main = expression(theta))
acf(1/PHI[,2], main = expression(sigma^2))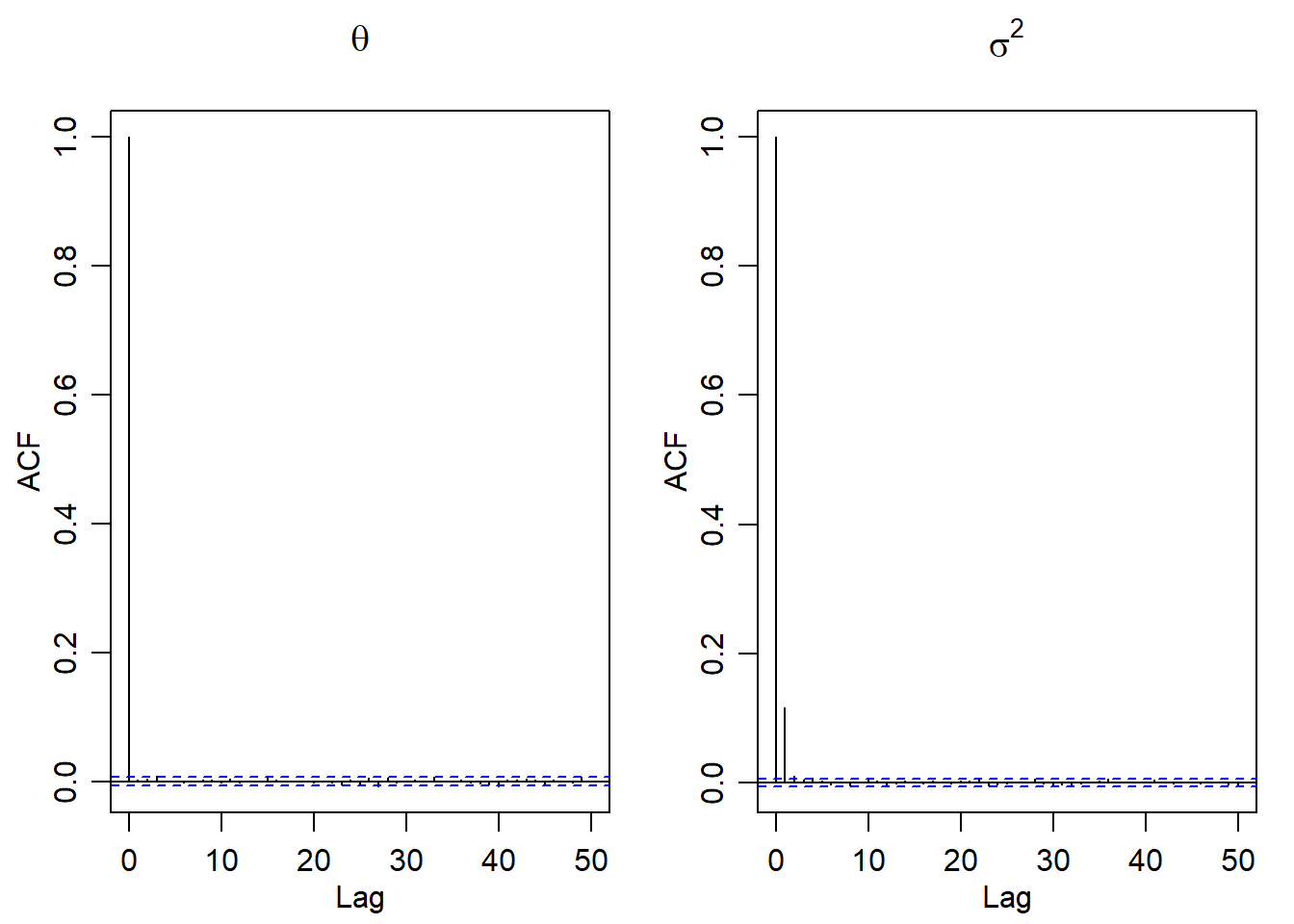
# tamaño efectivo de la muestraPodemos crear inferencias sobre los datos de la muestra
# intervalos de credibilidad
# media
round(quantile(PHI[,1], c(.025, 0.5, 0.975)), 3) 2.5% 50% 97.5%
1.711 1.805 1.901 # desviancion estandar
round(quantile(1/sqrt(PHI[,2]), c(.025, 0.5, 0.975)), 3) 2.5% 50% 97.5%
0.088 0.132 0.231 # probabilidad posterior
round(mean(PHI[,1] > 1.8), 3)[1] 0.5479 Regresion Bayesiana
Con los algoritmos bayesianos estudiados, nos permite realizar regresiones sobre los datos, pero a diferencia de la regresión lineal, esta nos permite construir la distribución de cada variable de la regresión.
Usaremos como ejemplo el salario, genero y años de experiencia de los gerentes bancarios
#devtools::install_github('pet-estatistica/labestData')
library(tidyverse)── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.2 ✔ tibble 3.2.1
✔ lubridate 1.9.4 ✔ tidyr 1.3.1
✔ purrr 1.0.4
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsBD<-labestData::CharnetEg7.3%>%
dplyr::mutate(gender=factor(sexo,labels=c('Female','Male')))%>%
dplyr::select(-sexo)
head(BD)%>%knitr::kable()| salario | exp | gender |
|---|---|---|
| 1.93077 | 0 | Female |
| 3.17692 | 17 | Female |
| 2.27692 | 5 | Female |
| 3.13077 | 15 | Female |
| 2.77692 | 9 | Female |
| 3.09231 | 15 | Female |
Podemos realizar una regresion lineal, una regresión lineal, es un modelo matemático que nos aproxima la relación de dependencia entre una variable dependiente \(Y\) y m variables independientes \(x_1,x_2,...,x_m\) más un error \(\epsilon \sim N(0,\sigma^2I)\).
Este tipo de método se puede aplicar en muchos casos para estudiar la relación entre dos o más variables, predecir el comportamiento de la variable \(Y\). En general el modelo de regresión lineal se puede expresar como:
\[Y=\beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_mx_m+\epsilon\] donde \(\beta_i\) es constante. y en particular el término \(\beta_0\) es la intersección.
Para realizar regresiones lineales, se usa la función lm()
Salarioslm <-lm(salario~exp+gender,data=BD)
summary(Salarioslm)
Call:
lm(formula = salario ~ exp + gender, data = BD)
Residuals:
Min 1Q Median 3Q Max
-0.35905 -0.08887 -0.00299 0.08037 0.18718
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.771484 0.050981 34.748 < 2e-16 ***
exp 0.090917 0.003436 26.461 < 2e-16 ***
genderMale 0.330990 0.056801 5.827 5.22e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1314 on 24 degrees of freedom
Multiple R-squared: 0.9784, Adjusted R-squared: 0.9766
F-statistic: 543 on 2 and 24 DF, p-value: < 2.2e-16library(ggplot2)
BD%>% ggplot(aes(y=salario,x=exp))+ geom_point(colour='orange3',alpha=0.65,size=1.5)+ geom_smooth(method='lm',colour='grey80')+ facet_wrap(~gender,scales='free')+ theme_bw()+ labs(y='Salary',x='Experience')`geom_smooth()` using formula = 'y ~ x'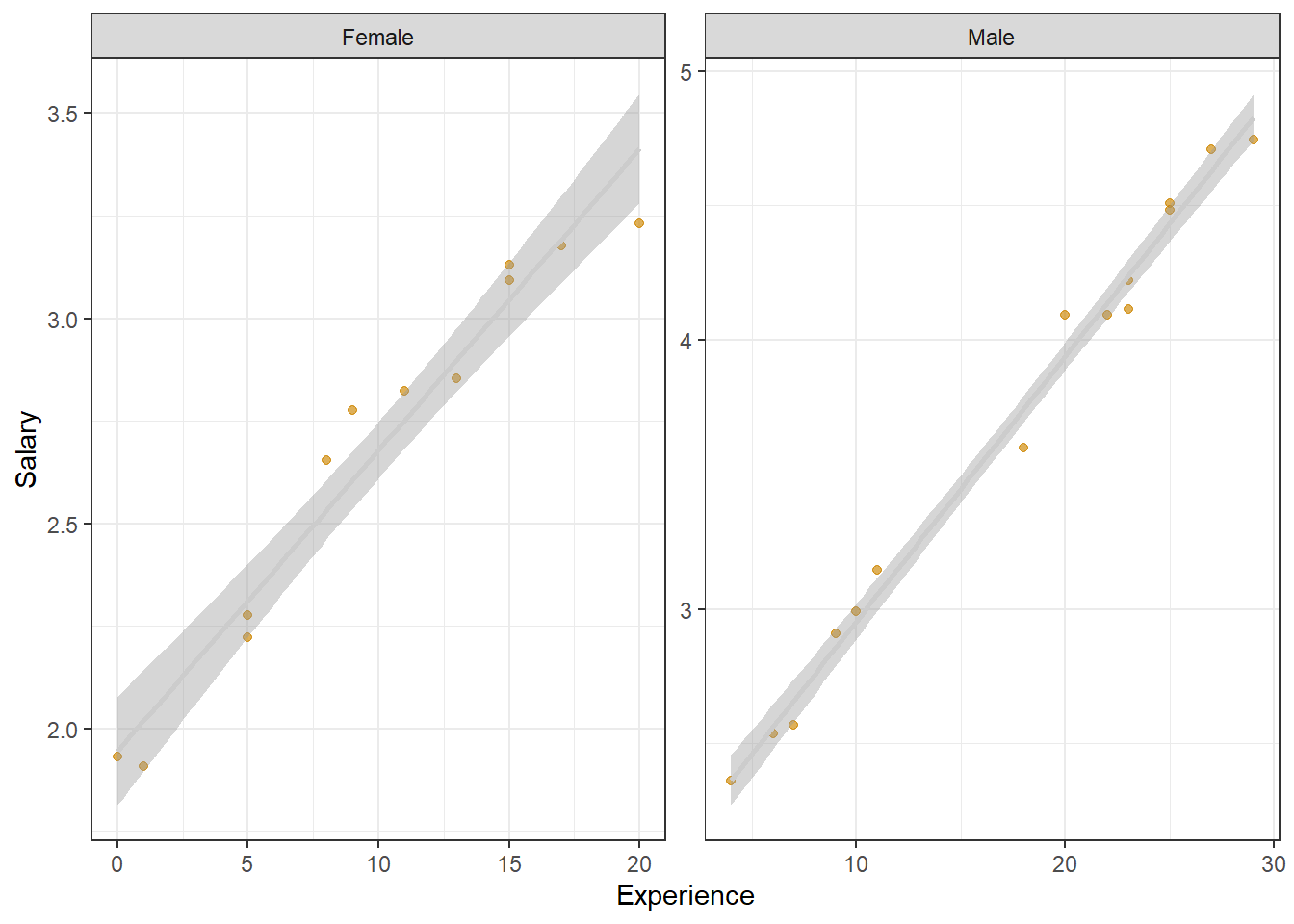
Para realizar la regresión lineal Bayesiana usaremos el paquete rstanarm y particular la función stan_glm, el enfoque de la regresión lineal Bayesiana consta en generar una distribución a posteriori de los parámetros \(\beta 's\) y el varianza \(\sigma^2\) del error.
library(rstanarm)
library(Rcpp)
model_bayes <- stan_glm(salario ~., data=BD)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 5.6e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.56 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.034 seconds (Warm-up)
Chain 1: 0.032 seconds (Sampling)
Chain 1: 0.066 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 1.5e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.15 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.04 seconds (Warm-up)
Chain 2: 0.03 seconds (Sampling)
Chain 2: 0.07 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 7e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.033 seconds (Warm-up)
Chain 3: 0.037 seconds (Sampling)
Chain 3: 0.07 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 7e-06 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.07 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.032 seconds (Warm-up)
Chain 4: 0.029 seconds (Sampling)
Chain 4: 0.061 seconds (Total)
Chain 4: print(model_bayes, digits = 3)stan_glm
family: gaussian [identity]
formula: salario ~ .
observations: 27
predictors: 3
------
Median MAD_SD
(Intercept) 1.770 0.053
exp 0.091 0.004
genderMale 0.333 0.061
Auxiliary parameter(s):
Median MAD_SD
sigma 0.136 0.020
------
* For help interpreting the printed output see ?print.stanreg
* For info on the priors used see ?prior_summary.stanregel valor MAD_SD es la Desviación Absoluta Mediana, calculada en la misma simulación. Usando el paquete bayesplot podemos realizar un MCMC de cada predictor.
library(bayesplot)
mcmc_dens(model_bayes, pars = c("exp"))+
vline_at(0.091, col="red")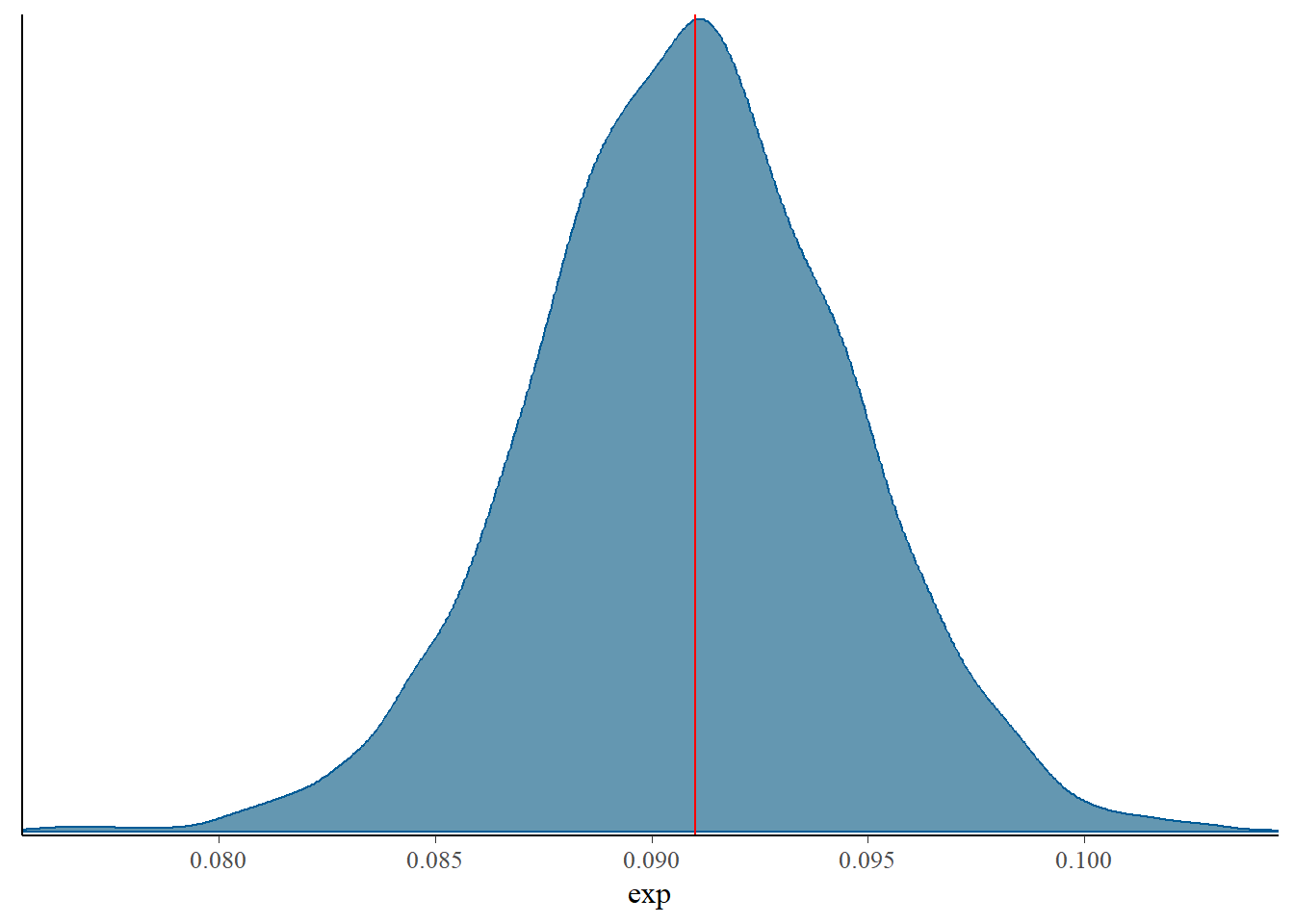
mcmc_dens(model_bayes, pars=c("genderMale"))+
vline_at(0.332, col="red")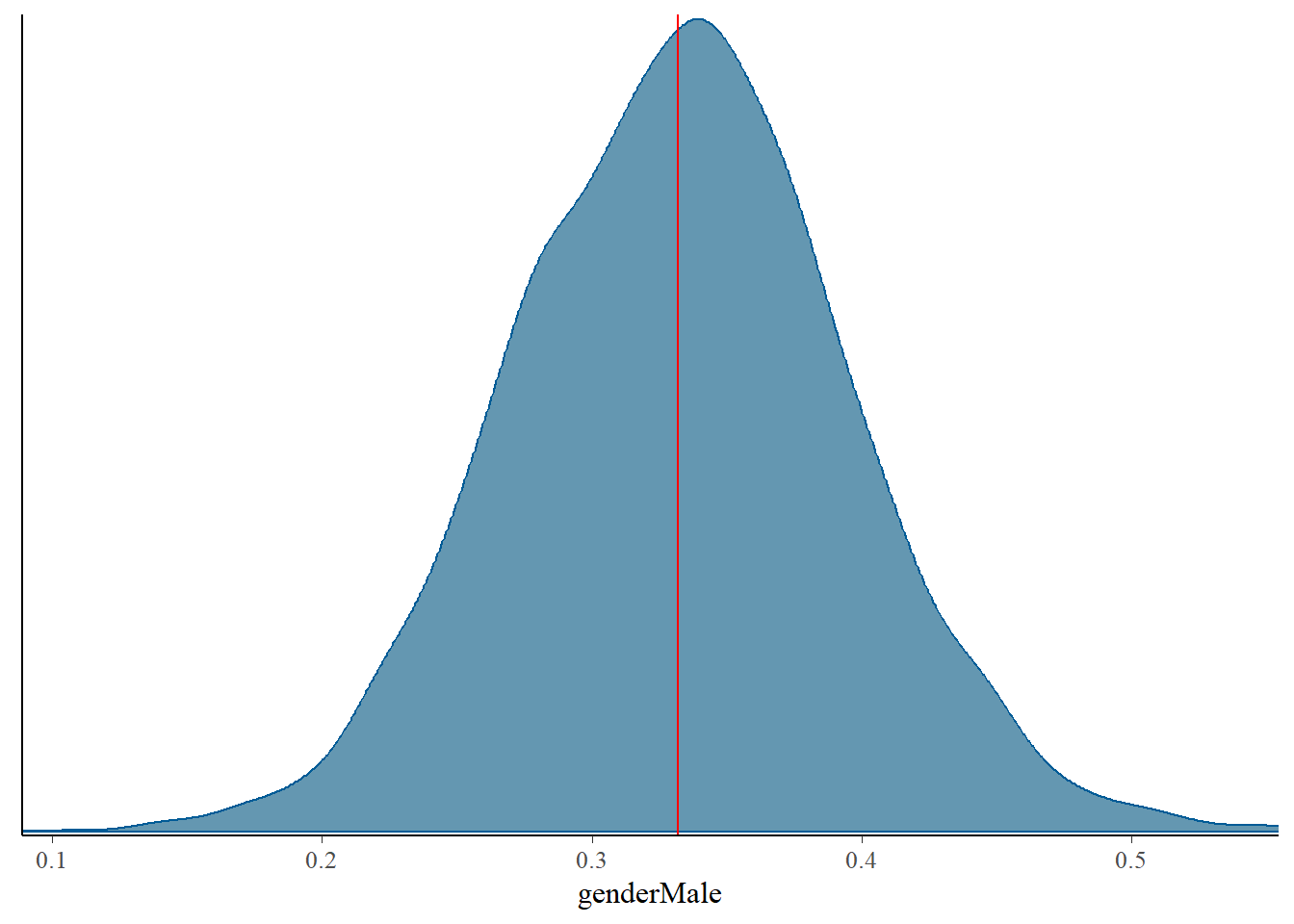
mcmc_dens(model_bayes, pars=c("(Intercept)"))+
vline_at(1.772, col="red")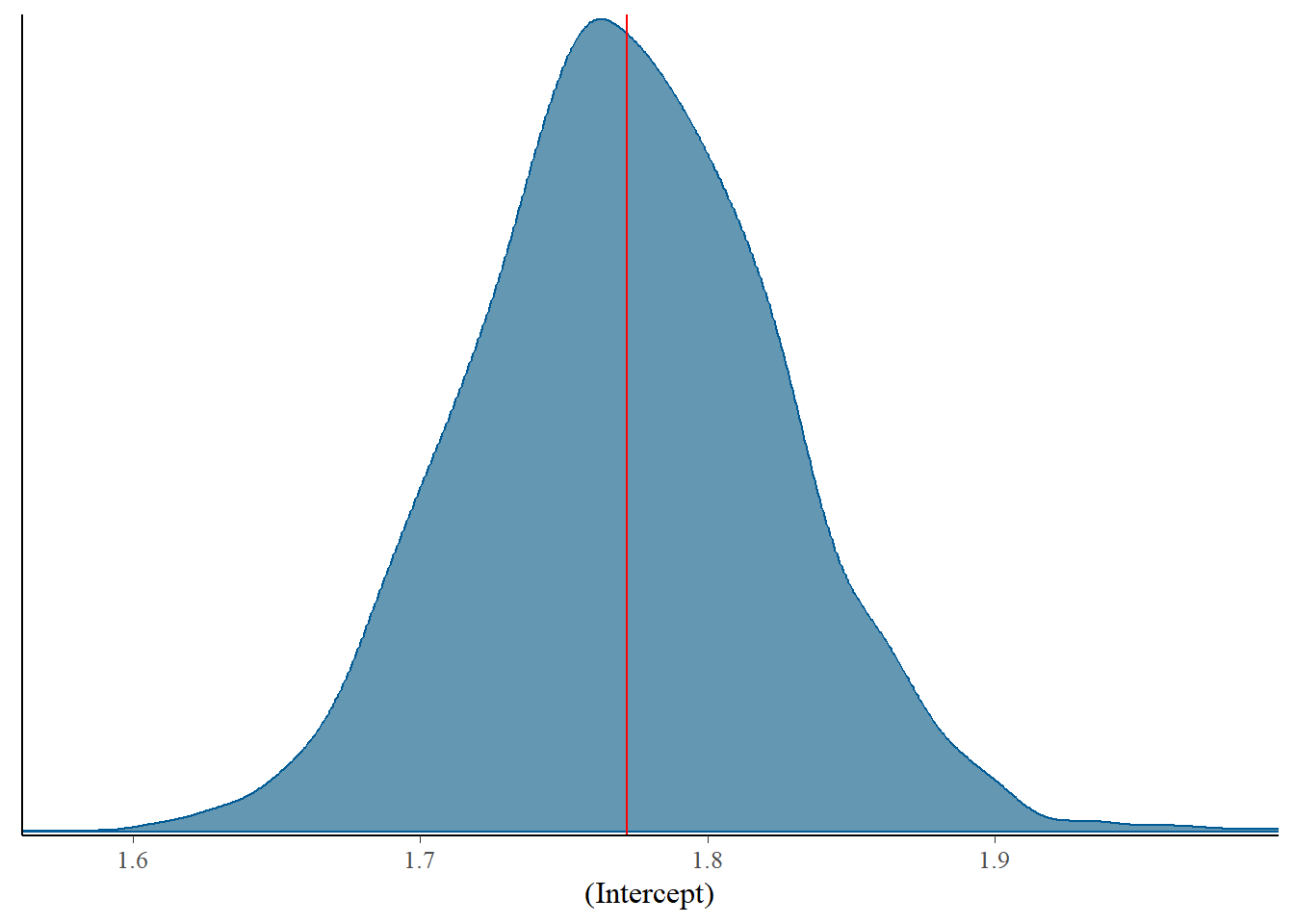
Para analizar el resultado de la regresión
library(bayestestR)
describe_posterior(model_bayes)Summary of Posterior Distribution
Parameter | Median | 95% CI | pd | ROPE | % in ROPE | Rhat | ESS
----------------------------------------------------------------------------------------
(Intercept) | 1.77 | [1.67, 1.88] | 100% | [-0.09, 0.09] | 0% | 1.001 | 4231.00
exp | 0.09 | [0.08, 0.10] | 100% | [-0.09, 0.09] | 5.84% | 1.000 | 2694.00
genderMale | 0.33 | [0.21, 0.45] | 100% | [-0.09, 0.09] | 0% | 1.001 | 3200.00donde:
Median es la mediana de la variable (parámetro)
CI es el intervalo de credibilidad, el porcentaje en este caso 95% indica que el 95% de los datos se encuentran dentro de este intervalo, en otras regresiones puede variar. A diferencia del intervalo de confianza dado un \(\alpha\) que nos indica que si repetimos varias veces un experimiento el \((1-\alpha)%\) de los datos estaría en este intervalo.
PD es la probabilidad de dirección, si es cercano a 1 indica que es su relación es positiva y si es cercana a 0 es negativa.
ROPE es un intervalo, donde nos indica que la variable puede valer 0, no tenga efecto.
% in Rope mide la probabilidad que esa variable sea 0.
Rhat: Factor de Reducción de Escala. Es una cantidad escalar, la desviación estándar de la variable de todas las cadenas juntas, dividida por la raíz cuadrada de la media de las desviaciones dentro de cada cadena separada, entre más cercano a 1 se considera que no hay problema de convergencia.
ESS tamaño de muestra efectivo, el umbral usual es de 400, y considera cuantas partes independientes contiene la misma cantidad de información que la muestra dependiente obtenidas en el MCMC, entre mayor se considera mejor.
Si observamos el intervalo CI, ninguna variable contiene el cero, por lo que podemos considerarlas a todas como significativas, en caso que alguna contenga el cero debe analizarse o por medio del intervalos HDI (Máxima densidad, o el intervalo de dos colas)
hdi(model_bayes)Highest Density Interval
Parameter | 95% HDI
--------------------------
(Intercept) | [1.67, 1.88]
exp | [0.08, 0.10]
genderMale | [0.21, 0.45]eti(model_bayes)Equal-Tailed Interval
Parameter | 95% ETI | Effects | Component
--------------------------------------------------
(Intercept) | [1.67, 1.88] | fixed | conditional
exp | [0.08, 0.10] | fixed | conditional
genderMale | [0.21, 0.45] | fixed | conditional