set.seed(2024)
x=rnorm(100,0,1)
barplot(x, ylim=c(-3,3), main="Datos de la muestra")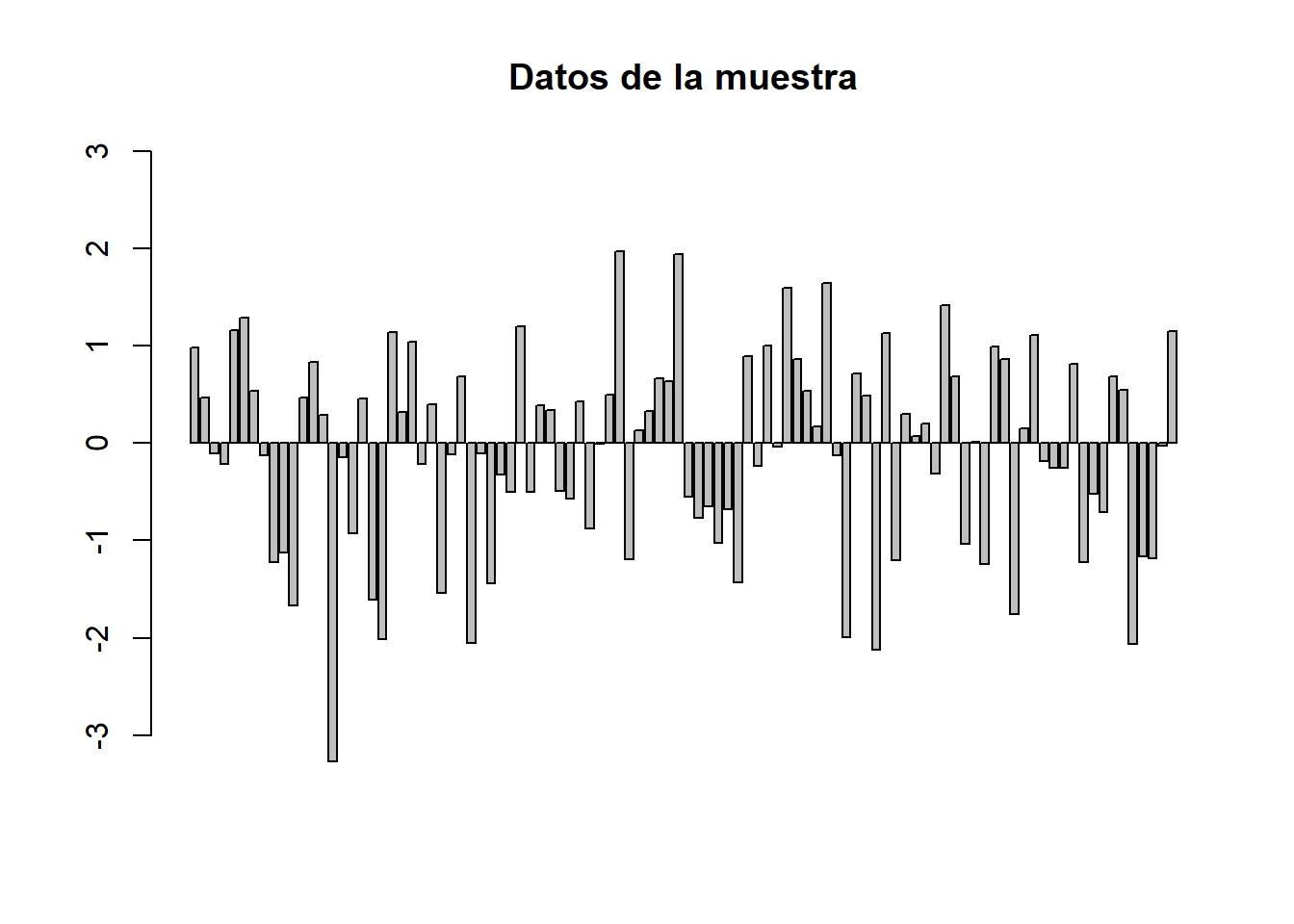
En muchos problemas estadísticos, nos interesa conocer la tendencia central de los datos de una población con el fin de encontrar ciertas características, en otras palabras nos interesa conocer la media, esperanza o promedio de los datos.
Pero en ocasiones, nos interera estimar el máximo o el mínimo para prever o disminuir riesgos.
Ejemplo
Diseño de plataformas marinas, rompeolas, diques entre otras construcciones portuarias u oceanicas, donde no nos interesa tanto el promedio del oleaje sino sus valores extremos.
En la construcción de edificios altos, lo importante a considerar son las velocidades máximas de viento o cargas máximas de peso en las edificaciones en general. O la capacidad de resistencia de terremotos.
En la construcción de represas hidroeléctricas nos interesa como conocer las inundaciones máximas.
En agricultura se requiere conocer los valores máximos de lluvia (inundaciones) y los niveles mínimos de lluvia (sequía).
En seguros para un manejo adecuado de provisiones se requiere conocer el máximo de reclamaciones de determinado seguro.
En Finanzas un problema común en las carteras de inversión es la máxima pérdida esperada.

Problema
Dada una muestra , esta presenta datos que podemos considerar atípicos, lo que nos puede llevar a realizarmos ciertas preguntas:
¿Es un dato erróneo?
¿Es un evento aislado?
¿Es repetible eventualmente?
¿ Una serie de valores extremos exhibe un comportamiento regular o una distribución en particular?
¿Cómo definimos un dato extremo de una muestra?
Definición
Sea \(X\) una variable aleatoria y \(u \in \mathbb{R}\). el valor de \(u\) se llama umbral y se dice que el evento \(X=x_i\) es un evento excedente en el nivel \(u\) si \(x_i \geq u\) y se dice que el evento es faltante en el \(u\) si \(x_i \leq u\)
Existen 3 modelos que son los más usados para analizar los datos extremos, estos según los datos que tenemos o el enfoque del analista.
Distribución de Orden (DOS)
Se utiliza cuando tenemos los datos completos de las muestras.
Valor Extremos Generalizados (GEV) o Von Mises
Se utiliza cuando tenemos sólo los datos de los máximos o mínimos, en este caso se utiliza una familia de distribuciones llamada Von Mises.
Por ejemplo: Se tiene registro únicamente las temperaturas máximas y mínimas por día.
Distribución de Pareto Generalizada
Se utiliza en estudios sobre datos excedentes o faltantes.
Usualmente los datos de una muestra están dados por el orden de la recolección de los datos, es decir por tiempo, o algún otro criterio, en esta metodología los reordenaremos de menor a mayor, esto podríamos perder cierta información relacionada con la captura de los datos.
Definición Sea m.a.s \(X=x_1,x_2,...,x_n\) de tamaño \(n\) con distribución \(F(X,\theta)\), se denomina el i-esimo estadístico de orden como \(x_{i:n}\).
En particular con los estadísticos de orden, podemos estimar:
El mínimo muestral igual \(x_{1:n}\)
El máximo máximo igual \(x_{n:n}\)
El rango muestral igual \(x_{n:n}-x_{1:n}\)
La mediana muestral es un estadístico de orden si \(n\) es impar y es igual a \(x_{(n+1)/2:n}\) y si n es par es igual a \(\frac{x_{(n+1)/2:n}+x_{(n)/2:n}}{2}\).
Ejemplo

Recordemos que para la variable aleatoria \(X\) con distribución \(F(X,\theta)\), la distribución \(F\) sigue una distribución Uniforme \(U[0,1]\). Para el valor \(x_{n:n}\) si conocemos la distribución \(F\) (o la aproximamos con una empírica) podemos encontrar su valor de probabilidad acumulada, es decir \(F(x_{n:n})\).
En el siguiente ejemplo, el valor máximo de la muestra fue 1.972819 y su probabilidad acumulada fue de 0.9757419.
set.seed(2024)
x=rnorm(100,0,1)
barplot(x, ylim=c(-3,3), main="Datos de la muestra")
Podemos reordenar la muestra de menor a mayor, según la estadística de orden
barplot(sort(x), ylim=c(-3,3), main="Datos de la muestra ordenados")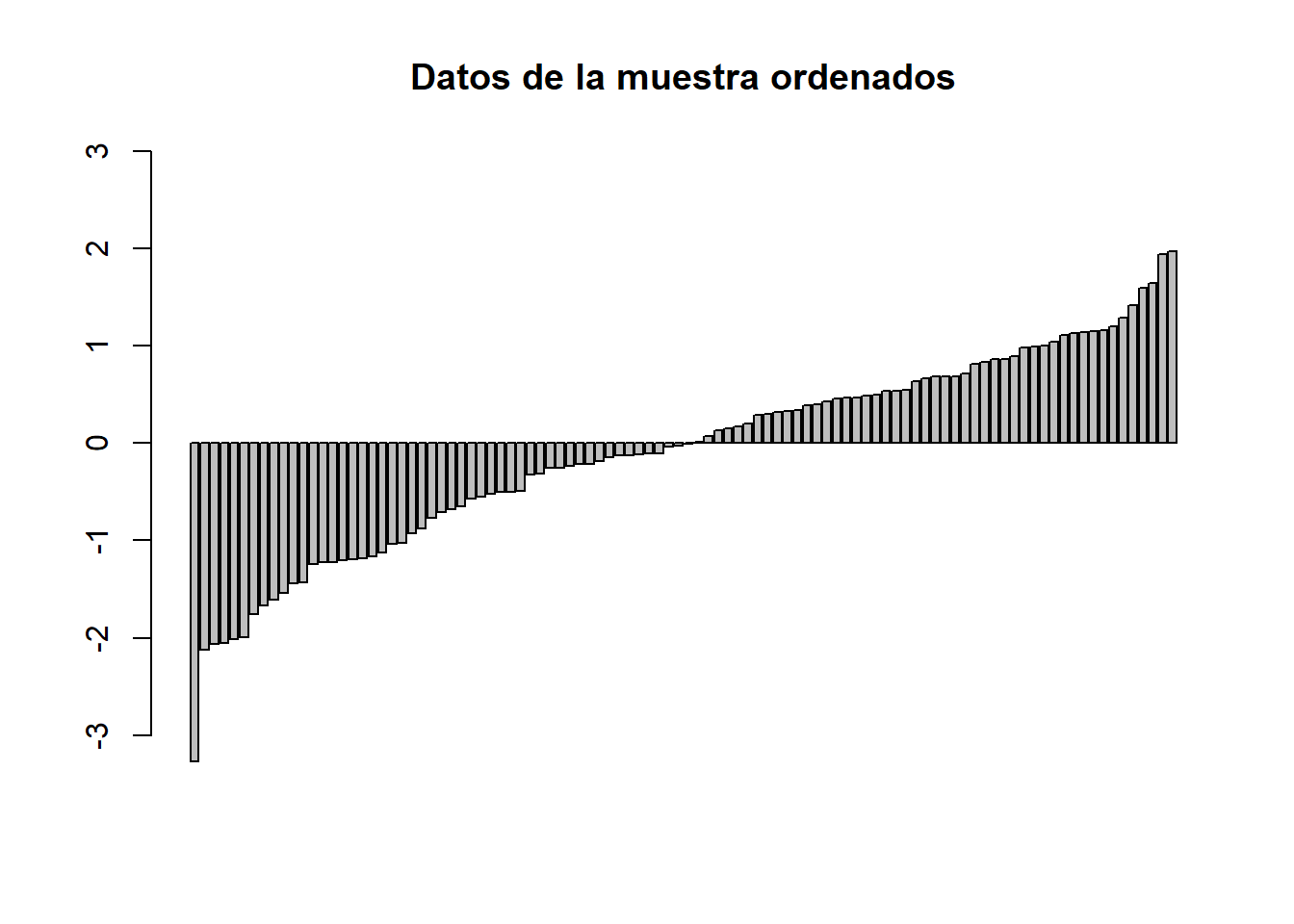
Estimamos la probabilidad acumula del máximo de la muestra y graficamos la distribución empírica.
(m=max(x))[1] 1.972819(Probaacumulada=pnorm(m))[1] 0.9757419plot(ecdf(x))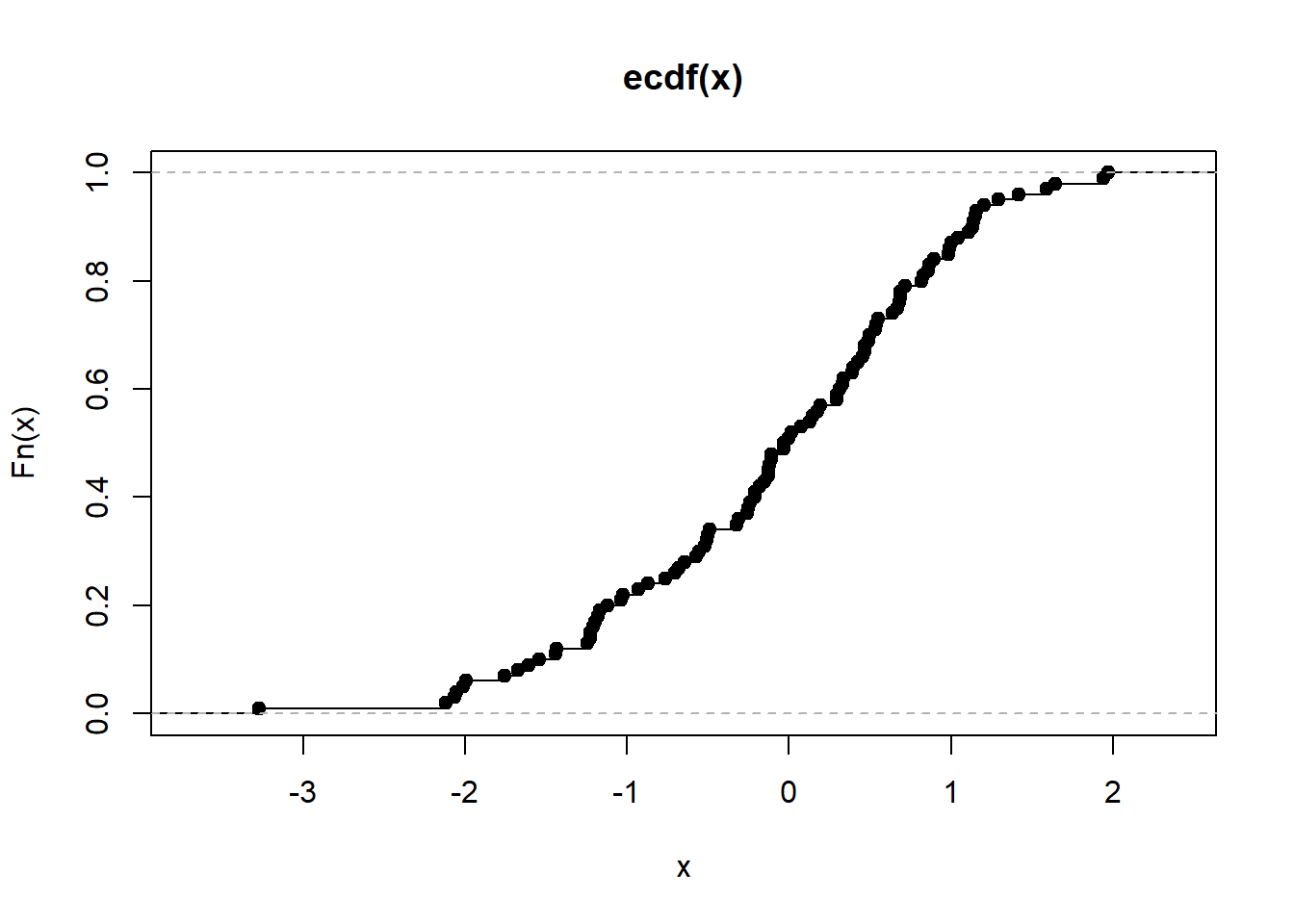
Si realizamos 100 muestras de una normal de media 0 y varianza 1, y gráficamos sus máximos y su probabilidad acumulada obtenemos los siguientes resultados:
set.seed(2024)
BD=matrix(rnorm(10000,0,1),nrow=100)
M=diag(BD[max.col(t(BD)),]) #Máximo por columnas.
Pacum=pnorm(M)
cat("media:")media:(media=mean(Pacum))[1] 0.9906417cat("mediana:")mediana:(mediana=median(Pacum))[1] 0.9944341#Densidad del Máximo
hist(Pacum, main="Histograma de la Probabilidad Acumulada")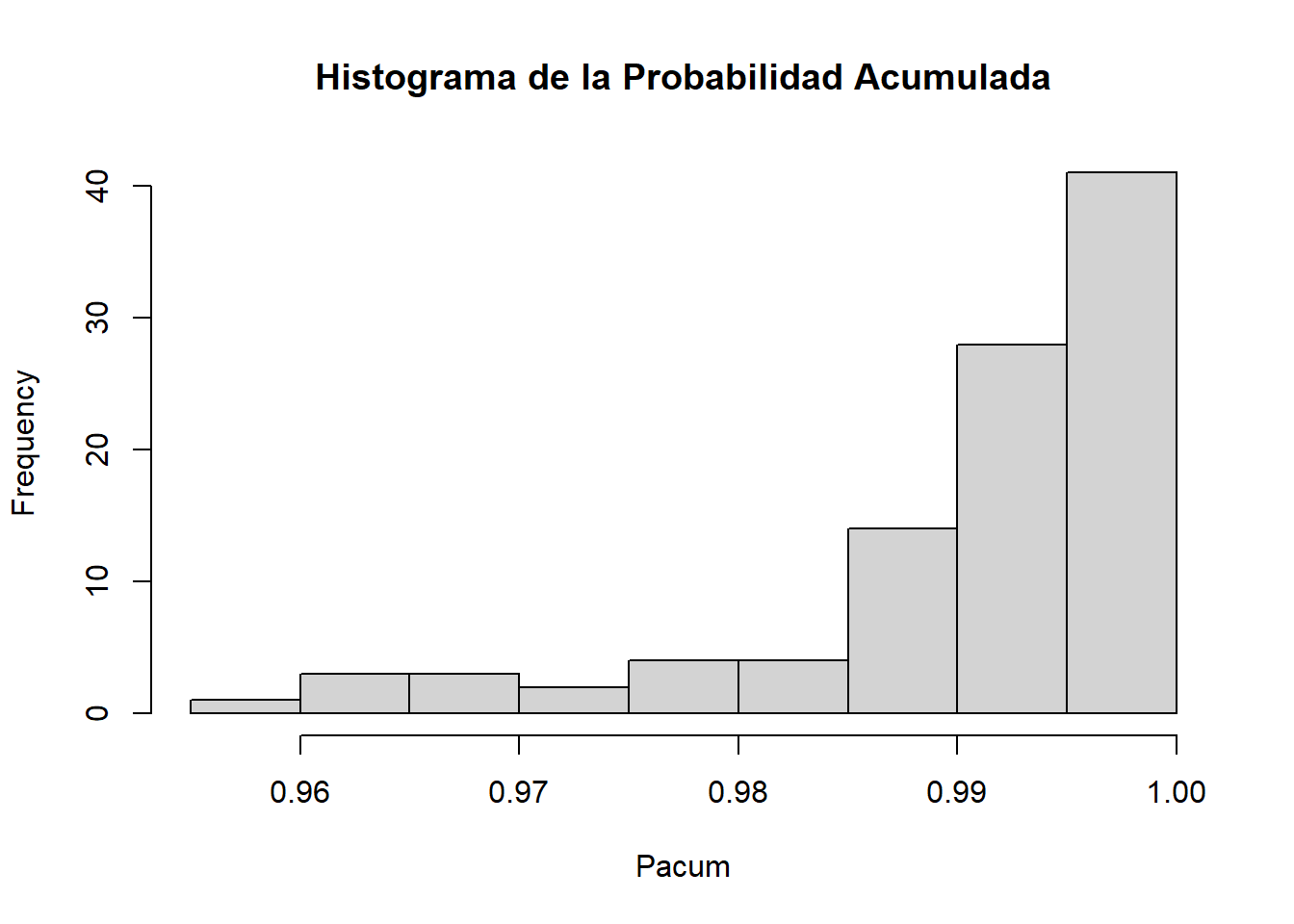
plot(density(Pacum),main="Densidad de la Probabilidad Acumulada")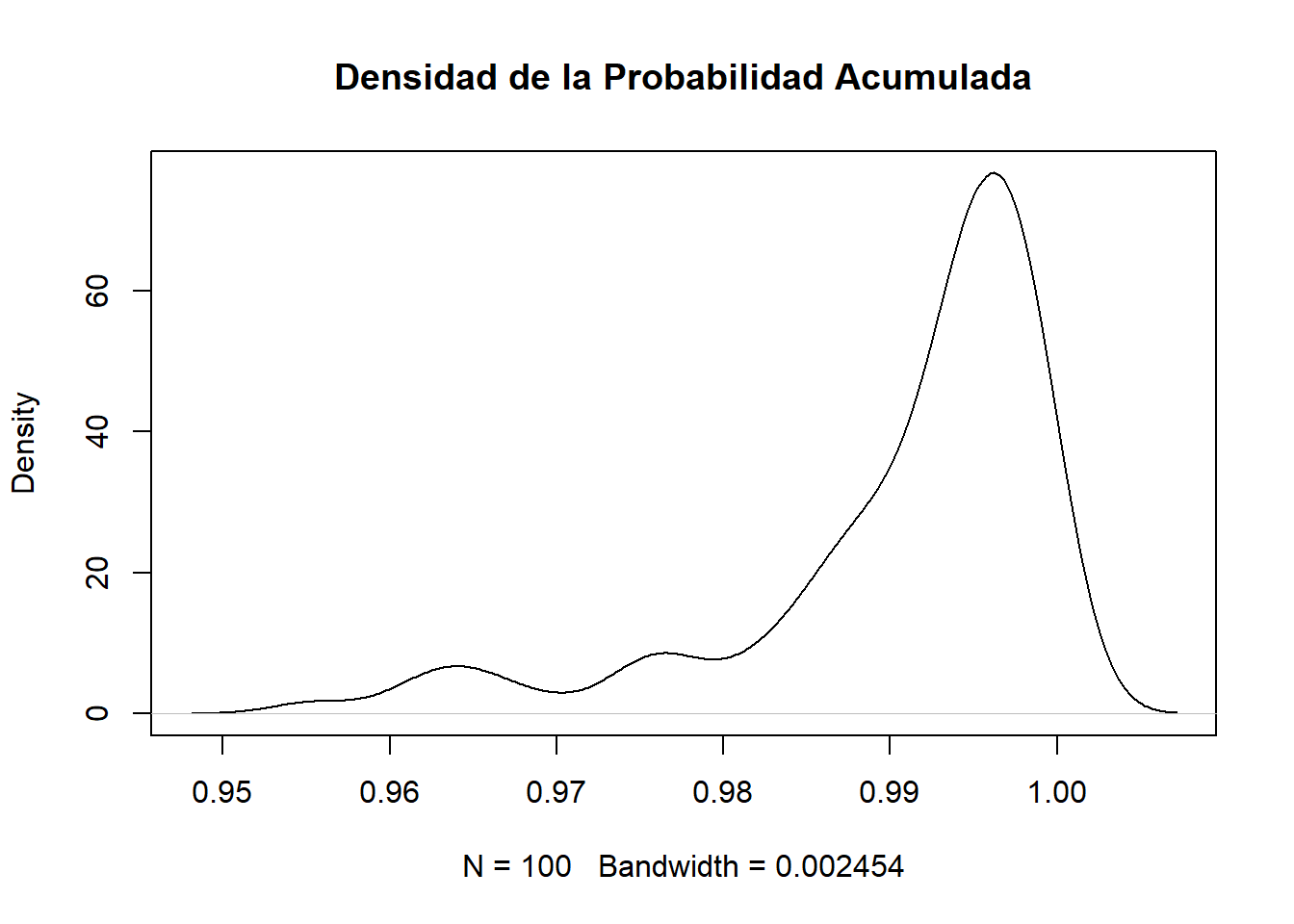
Esto nos muestra que el máximo posee una cola izquierda y una asimetría negativa, es decir la media esta a la izquierda (menor) de la mediana.
Los estadísticos de orden posee una distribución beta:
\[F(x_{i:n})=\beta (i,n+1-i)\] En particular para el máximo tenemos que se distribuye como una \(\beta (100,1)\).
plot(density(Pacum),main="Densidad de la Probabilidad Acumulada", ylim=c(0,100))
curve(dbeta(x, 100, 1), lwd=3, las=1, ylab='Densidad', add=TRUE)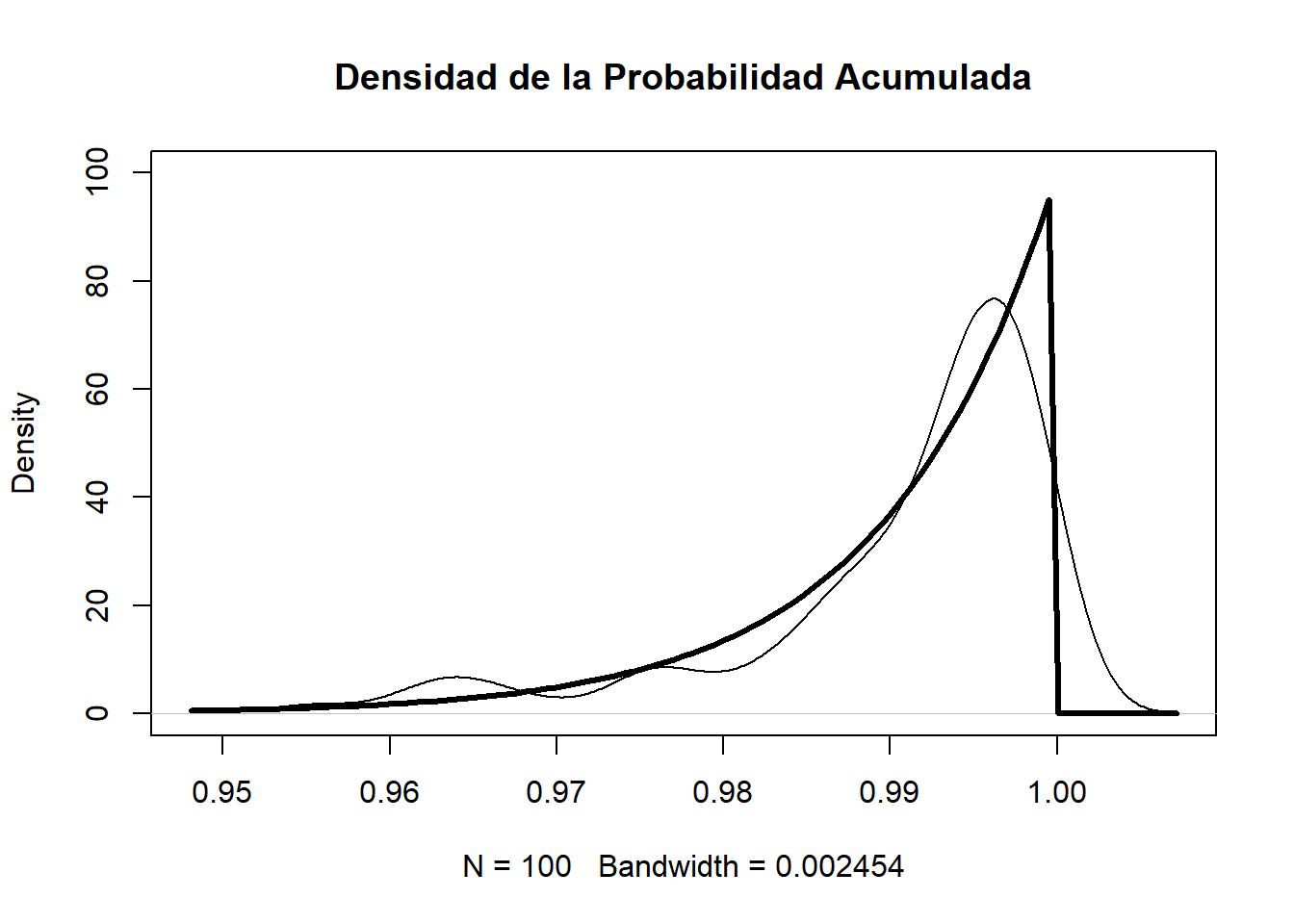
Al ser una distribución \(\beta\) tenemos que su esperanza (\(m_\beta\)) es \(\frac{\alpha}{\alpha+\beta}=\frac{i}{n+1}\), en particular para el valor máximo tenemos que su media sería de \(\frac{100}{101}=0.990099\), esto es llamado posición de Weibull.
Para el caso que estamos analizando, si tomamos \(F^{-1}(m_\beta)\), para nuestro ejemplo sería:
cat("valor maximo esperado:")valor maximo esperado:(qnorm(100/101))[1] 2.330079Ahora bien, supongamos que tenemos eventos de espera de cola, por ejemplo tiempo de atención de pacientes, supongamos que el tiempo medio de atención es de 10 minutos.
BD=matrix(rexp(10000,1/10),nrow=100) #Esperanza es 10.
M=diag(BD[max.col(t(BD)),]) #Máximo por columnas.
plot(M, main="Maximos de cada muestra")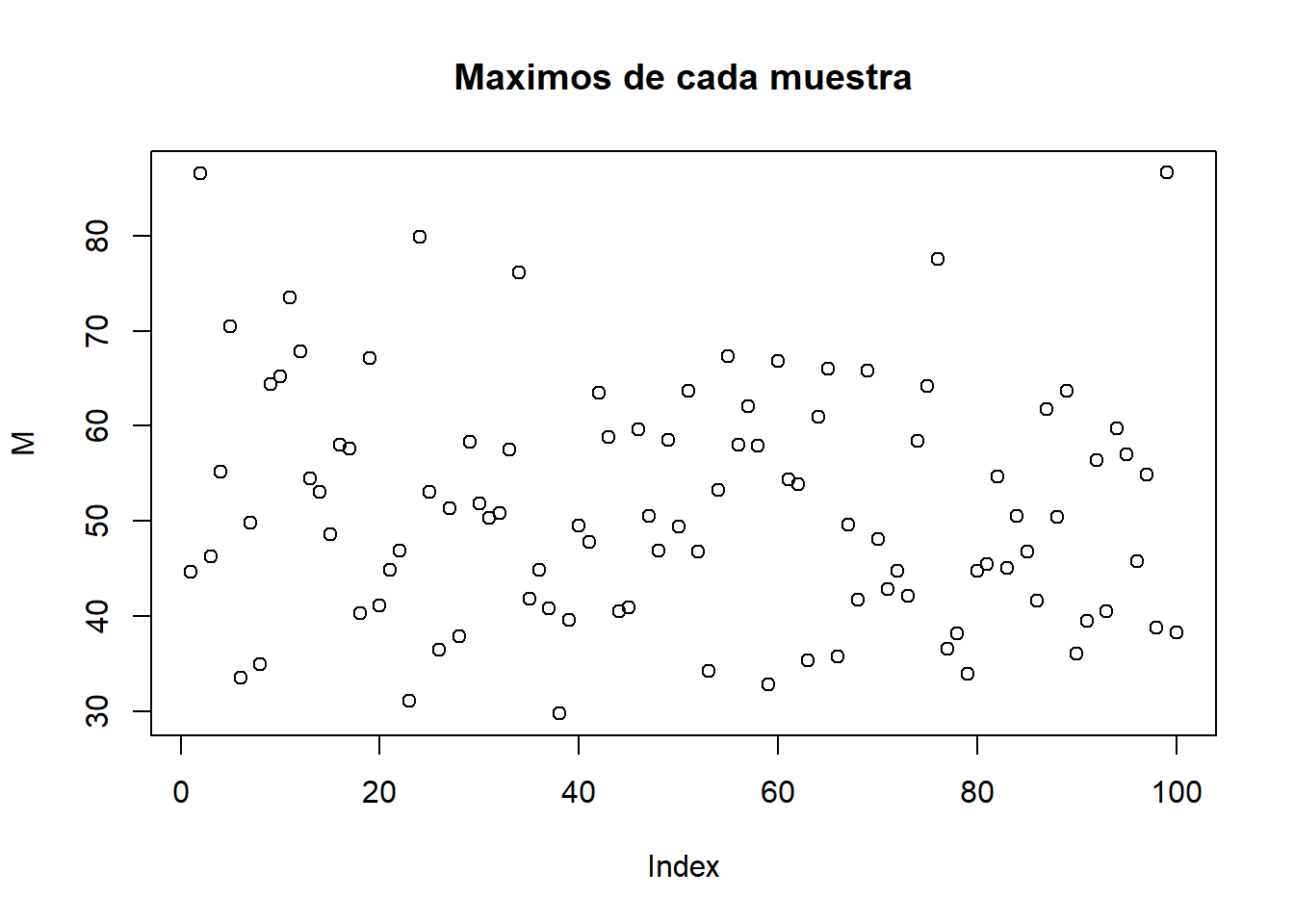
Pacum=pexp(M,1/10)
cat("media:")media:(media=mean(Pacum))[1] 0.9896175cat("mediana:")mediana:(mediana=median(Pacum))[1] 0.9935378#Densidad del Máximo
hist(Pacum, main="Histograma de la Probabilidad Acumulada")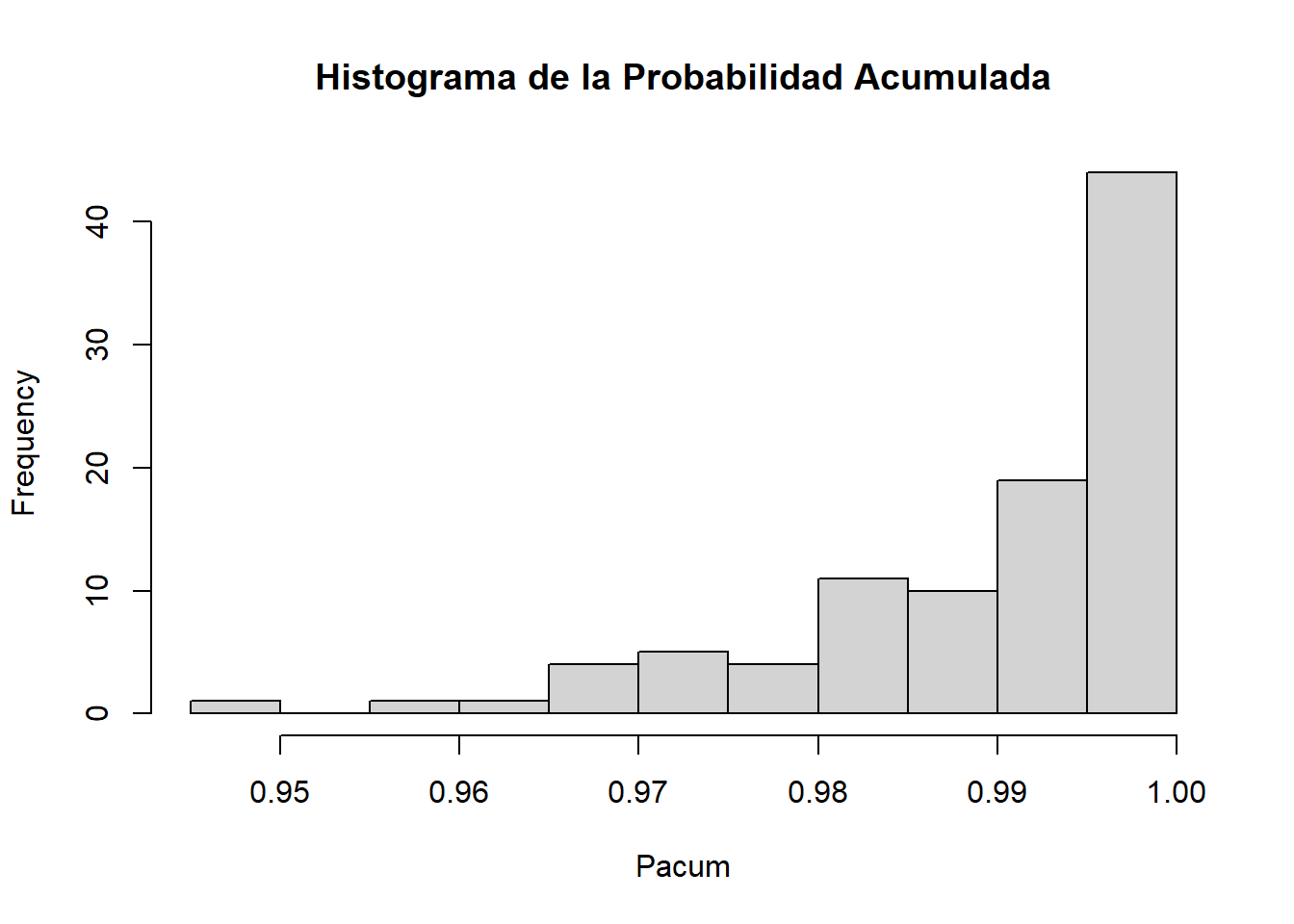
plot(density(Pacum),main="Densidad de la Probabilidad Acumulada",ylim=c(0,100))
curve(dbeta(x, 100, 1), lwd=3, las=1, ylab='Densidad', add=TRUE)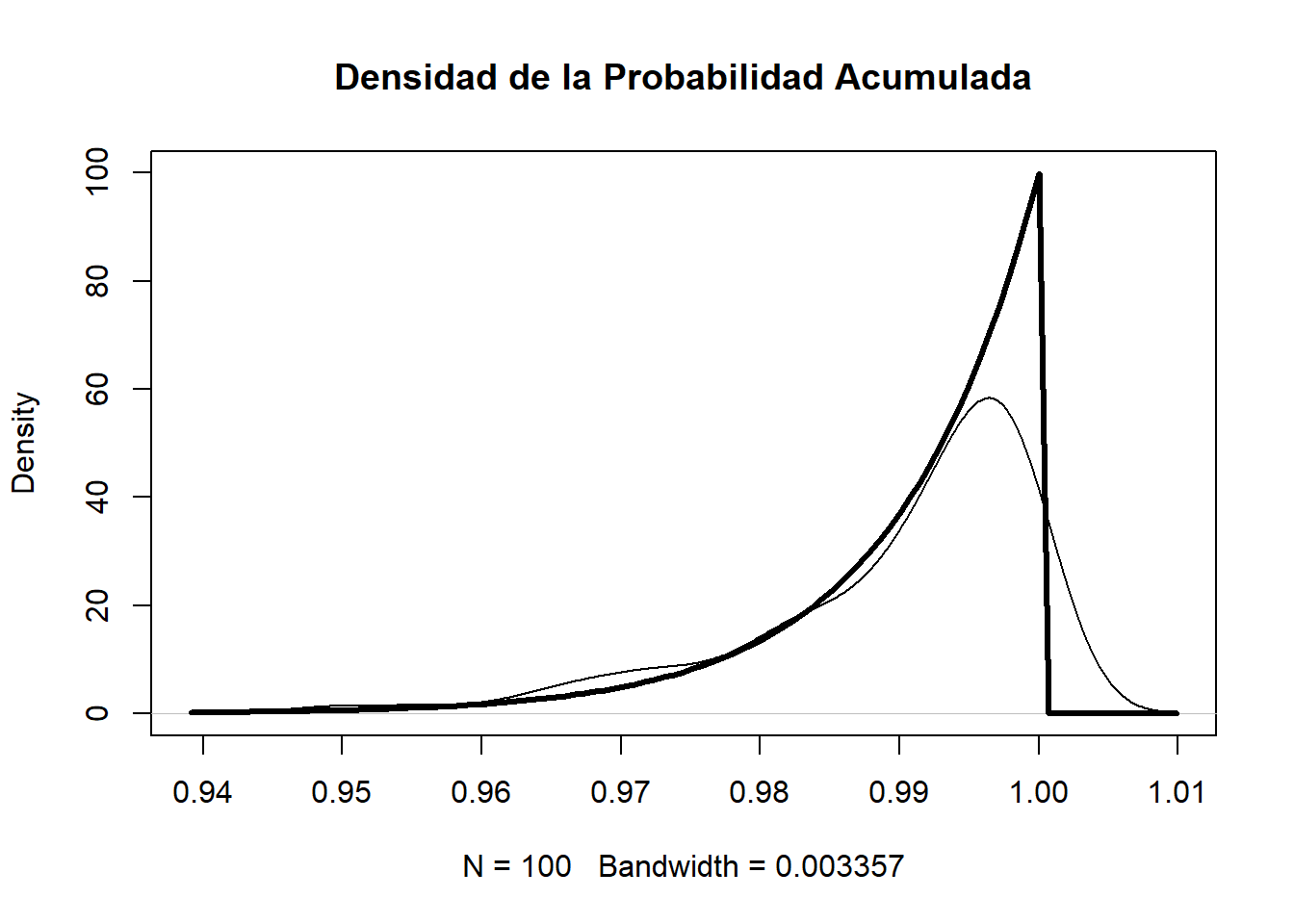
cat("valor maximo esperado:")valor maximo esperado:(qexp(100/101,1/10))[1] 46.15121Conclusiones del Modelo
Este procedimiento nos aproxima el valor de la probabilidad de los extremos y la podemos modelarlos con una distribución Beta, también podemos generalizar el método para cualquier otra posición de orden (cuantil).
Este modelo requiere que conozcamos la distribución \(F\) y al menos el tamaño de las muestras \(n\).
Las distribuciones de valores extremos son formalmente distribuciones límites para máximos, dada una secuencia de variables aleatorias. Suponiendo que \(X_1,...,X_n\) es una m.a.s con una función de distribución \(F\). La función de distribución del máximo (\(M_n\)) esta dada por:
\[P(M_n \leq x)=P(X_1\leq x_1,...X_n\leq x_n)=P(X_1\leq x_1)\cdots P(X_n\leq x_n)=F^n(x)\] Si \(F\) es desconocida y se desea conocer \(M_n\) entonces esta fórmula, no aporta a la solución del problema, pero aunque no conozcamos \(F\), asintóticamente si se puede deducir la distribución de \(M_n\).
Si normalizamos con sucesiones \(a_n\) y \(b_n\) adecuadas para \(M_n\) tenemos que:
\[P\left(\frac{M_n-b_n}{a_n}\leq x \right)=P(M_n\leq a_nx+b_n)=F^n(a_nx+b_n)\to H(x),n\to \infty\]
Donde \(H(x)\) es una distribución no degenerada, es decir que no toma siempre valores de 1 o 0, si esto ocurre se dice que \(F(x)\) pertenece al máximo dominio de atracción (MDA) de \(H\), y lo denotamos como \(F \in MDA(H)\).
Primer Teorema Fundamental de GEV (Fisher, Tippet, Gnedenko)
Sea \(F\) una función de distribución tal que \(F \in MDA(H)\), entonces \(H\) puede estandarizarse de manera única (variando las sucesiones \(a_n\) y \(b_n\)).
Ejemplo
Consideremos la distribución exponencial
\[F(x)=1-e^{-\beta x}\]
para \(\beta >0\), \(x \geq 0\), si tomamos \(a_n=1/\beta\) para todo \(n\) y \(b_n=ln(n)/\beta\), entonces
\[\lim_{n\to \infty}F^n(a_nx+b_n)=\lim_{n\to \infty}\left(1+\frac{1}{n}e^{-x} \right)^n=e^{e^{-x}}\] Por lo que si tomamos \(H(x)=e^{e^{-x}}\), \(F \in MDA(H)\) y esta normalización es única.
Resuelta que hay sólo tres tipos de valores de distribución de extremos ( máximo o mínimos) a pesar de los datos de entrada, esto lo demostraron Fisher y Tippet en 1928. Esta distribuciones en su forma estándar son:
Gumbel
\[H(x)=e^{e^{-x}}, \quad -\infty < x< \infty\]
Weibull
\[ H(x)=\begin{cases} e^{x} & x < 0 \\ 1 & x \geq 0 \end{cases} \] Fréchet
\[ H(x)=\begin{cases} e^{-x^{-1}} & x >0 \\ 0 & x \leq 0 \end{cases} \]
Estas tres distribuciones son llamadas distribuciones de valores extremos, y el teorema fundamental señala que si la convergencia existe del límite, entonces pertenece alguna de estas familias.
Podemos generalizar estas distibuciones, agregando un parámetro de localización \(\mu\), uno de forma \(\sigma\) y de escala \(\alpha\), de forma que:
Gumbel
\[H(x,\mu,\sigma)=e^{e^{-(x-\mu)/\sigma}}, \quad -\infty < x< \infty, \sigma>0\]
Weibull
\[ H(x,\mu,\sigma, \alpha)=\begin{cases} e^{-(-(x-\mu)/\sigma)^{\alpha}} & x < \mu \\ 1 & x \geq \mu \end{cases} \] con \(\alpha >0\)
Fréchet
\[ H(x,\mu,\sigma, \alpha)=\begin{cases} e^{-((x-\mu)/\sigma)^{-\alpha}} & x >\mu \\ 0 & x \leq \mu \end{cases} \] con \(\alpha >0\)
Observe que el parámetro \(\mu\) es el extremo izquierdo para la distribución de Fréchet y el extremo externo para la distribución de Weibull.
Von Mises en 1954, generaliza las distribuciones de valores extremos en una sola distribución llamada Distribución de Valores Extremos Generalizados (GEV), de ahí que también se conoce las distribuciones de valores extremos como distribuciones de Von Mises, esta distribución se plantea de la siguiente manera:
\[ H(x,\xi)=\begin{cases} e^{-(1+\xi x)^{1/\xi})} & 1+\xi x >0,\quad \xi \neq 0 \\ e^{-e^{-x}} & \quad \xi = 0 \end{cases} \]
Si se toma los parámetros de localización \(\mu\) y de forma \(\sigma\), el valor de \(\xi\) es la escala, entonces podemos generalizarla como
\[H(x,\mu,\sigma,\alpha)=H((x-\mu)/\sigma,\xi)\] Observe que si \(\xi <0\) estamos ante la distribución de Weibull, y si \(\xi >0\) estamos en el caso de la distribución de Fréchet, y con \(\xi=0\) es la distribución de Gumbel.
Ejemplo
Se muestra diferentes gráficos de las distribuciones de valores extremos, usando el paquete “evd”
library(evd) #Gumbel
x=seq(-4,4,0.1)
M1<-dgumbel(x,0,1) #n, localización y forma
M2<-dgumbel(x,1,1)
M3<-dgumbel(x,1,2)
M4<-dgumbel(x,2,2)
plot(x,M1,main="Gumbel",col="blue",type="l")
lines(x,M2,col="red")
lines(x,M3,col="green")
lines(x,M4,col="gold")
legend("topleft", legend = c("mu=0, sigma=1", "mu=1, sigma=1","mu=1, sigma=2","mu=2, sigma=2"), col = c("blue", "red","green","gold"),lty = c("solid", "solid","solid","solid"))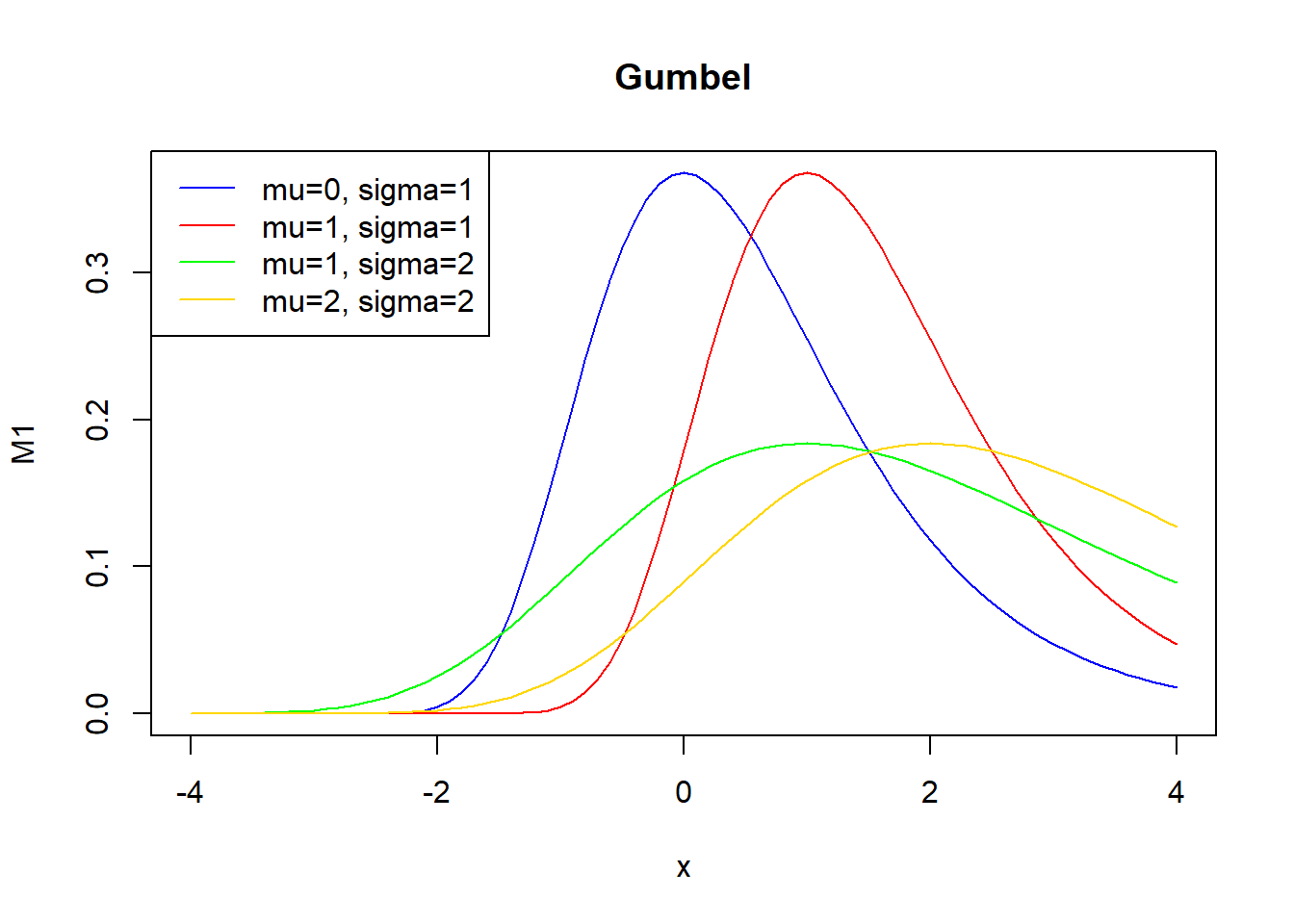
#frechet
x=seq(-4,4,0.1)
M1<-dfrechet(x,0,1,1) #n, localización, forma, escala
M2<-dfrechet(x,0,1,0.8)
M3<-dfrechet(x,0,1,0.5)
M4<-dfrechet(x,0,1,0.1)
plot(x,M1,main="Frechet-mu=0,sigma=1",col="blue",type="l",ylim=c(0,0.7))
lines(x,M2,col="red")
lines(x,M3,col="green")
lines(x,M4,col="gold")
legend("topleft", legend = c("alpha=1", "alpha=0.8","alpha=0.5","alpha=0.1"), col = c("blue", "red","green","gold"),lty = c("solid", "solid","solid","solid"))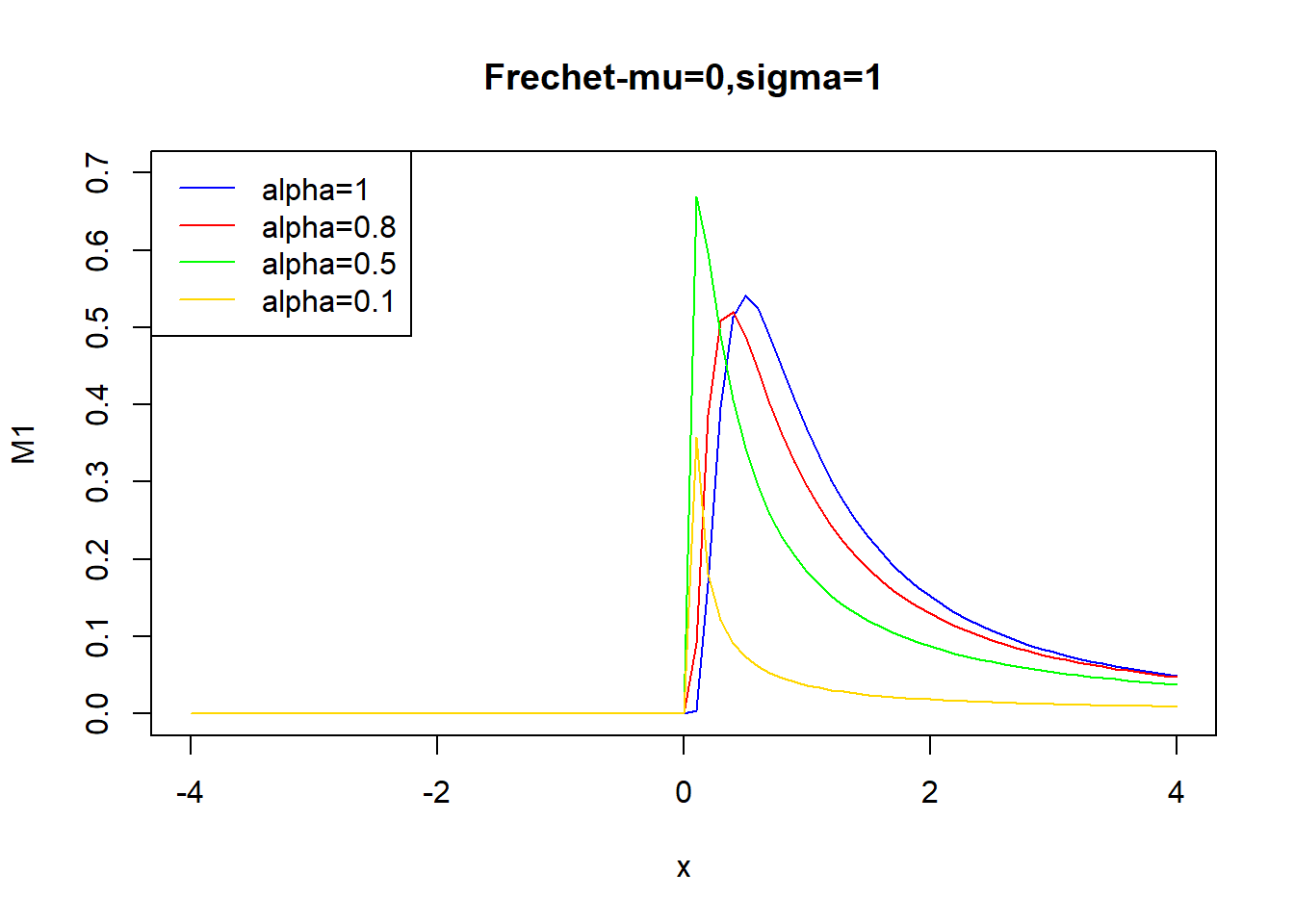
library(evd) #Weibull
x=seq(-4,4,0.1)
M1<-drweibull(x,0,1,1) #n, localización, forma, escala
M2<-drweibull(x,0,1,0.8)
M3<-drweibull(x,0,1,0.5)
M4<-drweibull(x,0,1,0.1)
plot(x,M1,main="Weibull-mu=0, sigma=1",col="blue",type="l",ylim=c(0,1))
lines(x,M2,col="red")
lines(x,M3,col="green")
lines(x,M4,col="gold")
legend("topleft", legend = c("alpha=1", "alpha=0.8","alpha=0.5","alpha=0.1"), col = c("blue", "red","green","gold"),lty = c("solid", "solid","solid","solid"))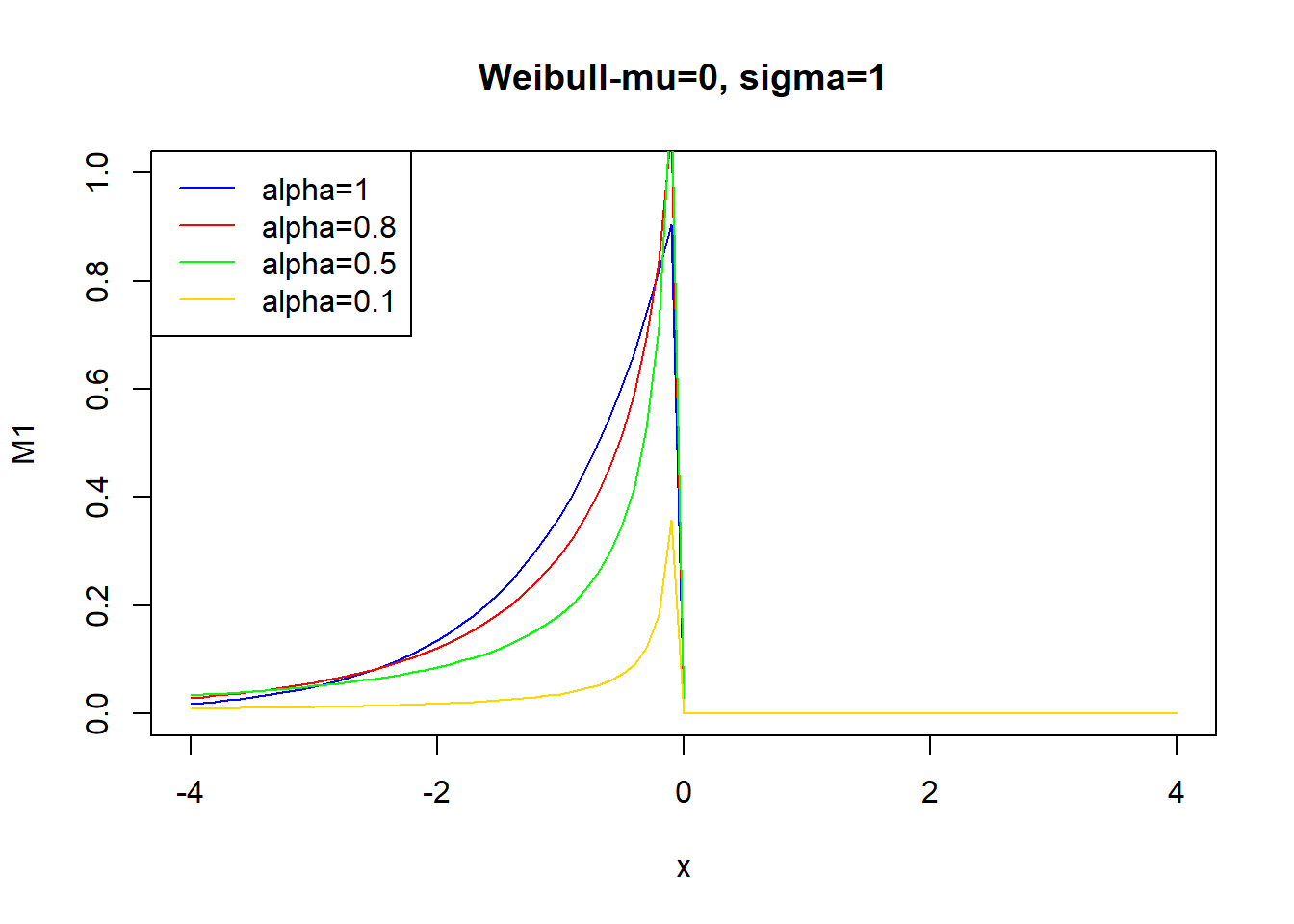
library(evd) #GEV
x=seq(-4,4,0.1)
M1<-dgev(x,0,1,0.5) #n, localización, forma, escala
M2<-dgev(x,0,1,-0.5)
M3<-dgev(x,0,1,0.8)
M4<-dgev(x,0,1,-0.8)
plot(x,M1,main="GEV-mu=0, sigma=1",col="blue",ylim=c(0,1),type="l")
lines(x,M2,col="red")
lines(x,M3,col="green")
lines(x,M4,col="gold")
legend("topleft", legend = c("alpha=0.5", "alpha=-0.5","alpha=0.8","alpha=-0.8"), col = c("blue", "red","green","gold"),lty = c("solid", "solid","solid","solid"))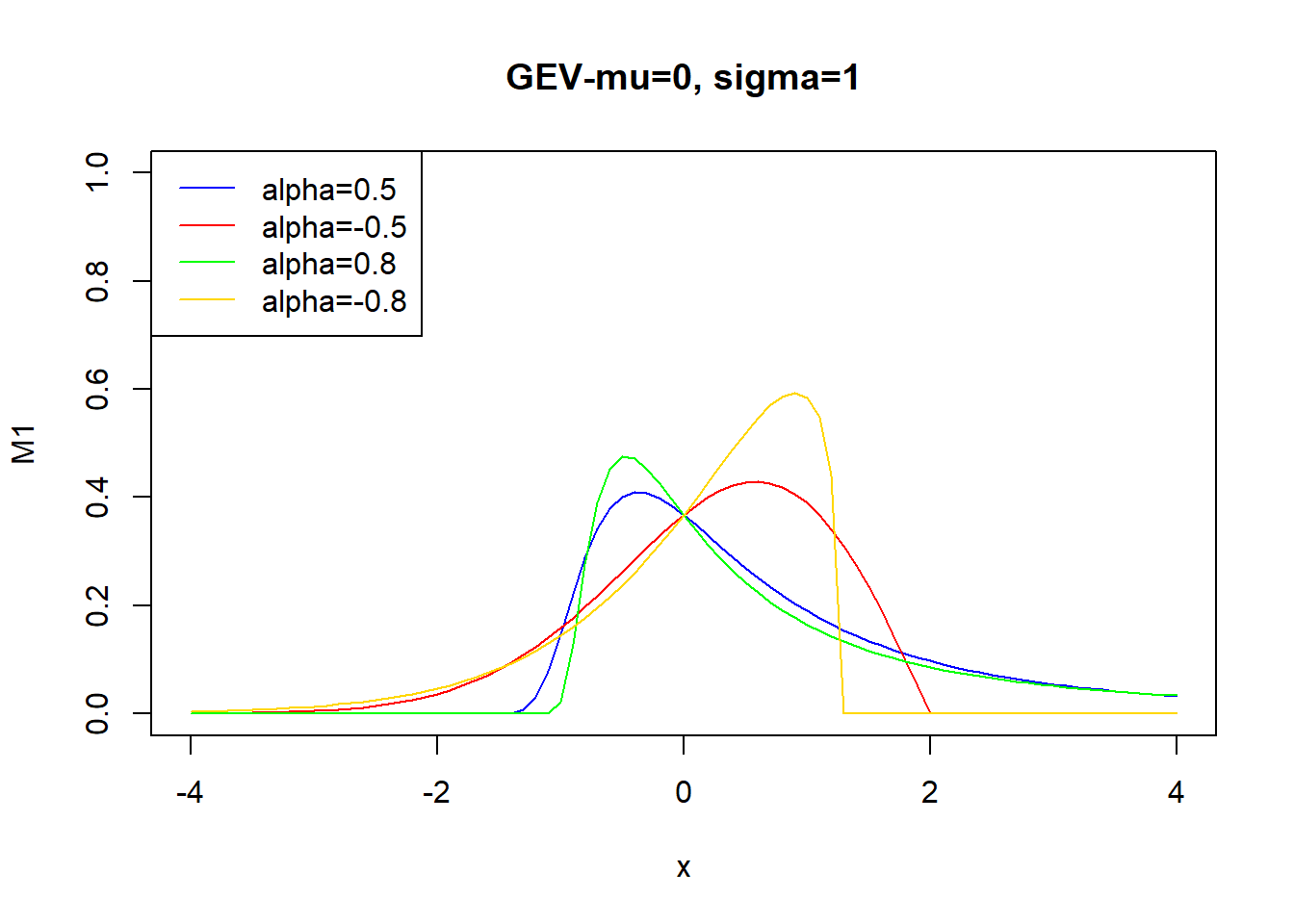
En la siguiente tabla podemos encontrar un resumen de las distribuciones comunes y sus distribuciones de los extremos
| Distribución | Máximo | Mínimo |
|---|---|---|
| Exponencial | Gumbel | Weibull |
| Gamma | Gumbel | Weibull |
| Normal | Gumbel | Gumbel |
| log-Normal | Gumbel | Gumbel |
| Pareto | Fréchet | Weibull |
| Cauchy | Fréchet | Fréchet |
Una forma de encontrar los parámetros de la distribución GEV en general es usar la función fgev, esta se baja en un proceso de máxima verosimilitud de los parámetros de GEV.
Ejemplo
Tomemos por ejemplo una distribución Normal con media 0 y varianza 1, para un total de 10 000 datos divididos en bloques de 100, también podemos pensar que son 100 muestras de longitud 100.
library(evd) #GEV
set.seed(2024)
BD=matrix(rnorm(10000,0,1),nrow=100)
M=diag(BD[max.col(t(BD)),]) #Máximo por columnas.
(gev1<-fgev(M))
Call: fgev(x = M)
Deviance: 91.8174
Estimates
loc scale shape
2.3667 0.3733 -0.2224
Standard Errors
loc scale shape
0.04083 0.02817 0.05500
Optimization Information
Convergence: successful
Function Evaluations: 64
Gradient Evaluations: 13 El resultado de la muestra, nos da como resultado una GEV con valores de \(\mu=2.3667\),\(\sigma=0.3733\) y \(\xi=-0.2224\), podemos generar una muestra con estos valores para estimar nuestro valor extremo esperado.
\[ E[X]=\begin{cases} \mu+\frac{\sigma(\Gamma(1-\xi)-1)}{\xi} &\text{si } \xi\neq 0,\xi < 1,\\ \mu+\sigma\gamma &\text{si } \xi= 0,\\ \infty &\text{si } \xi\geq 1 \end{cases} \]
donde \(\gamma\approx 0.57721\) la constante de Euler-Mascheroni.
Para nuestro ejemplo, sería:
(Esp=2.3667+(0.3733*(gamma(1-(-0.2224))-1)/(-0.2224)))[1] 2.513518Ejemplo
Tomemos por ejemplo una distribución Exponencial con esperanza igual a 10
library(evd) #GEV
BD=matrix(rexp(10000,1/10),nrow=100)
M=diag(BD[max.col(t(BD)),]) #Máximo por columnas.
(gev1<-fgev(M))
Call: fgev(x = M)
Deviance: 776.9741
Estimates
loc scale shape
46.23947 10.49567 -0.08371
Standard Errors
loc scale shape
1.19616 0.86791 0.08023
Optimization Information
Convergence: successful
Function Evaluations: 22
Gradient Evaluations: 7 Similarmente podemos estimar su valor máximo
(Esp=44.76948+(9.39585*(gamma(1-(0.03915))-1)/(0.03915)))[1] 50.57038El último método para estimar los valores extremos esperados, es Pareto Generalizado, como se indicó este considera los datos excedentes o faltantes de un determinado umbral, esto se debe a que con el método de estadísticas de orden o de GEV, consideramos únicamente el máximo de cada bloque, lo que se conoce como Método de Bloque Máximo.
El método de Pareto Generalizado, considera otros eventos importantes dentro de los bloques, lo que significa que considera la información de máximos locales ( excedentes de nivel \(u\)) dentro de un bloque:
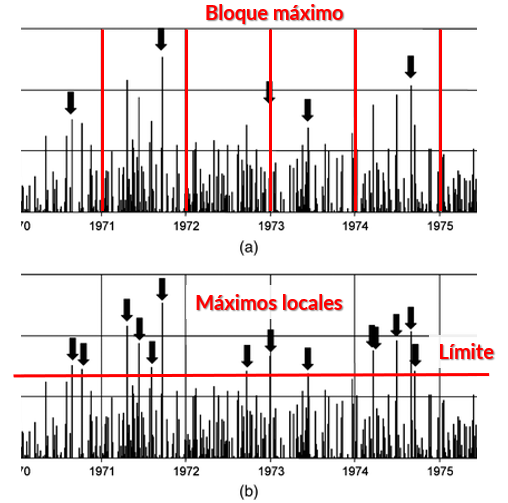
Esta situación de considerar los máximos locales en cada bloque, ocasiona que al final tendremos más máximos que bloques establecidos.
Segundo Teorema Fundamental de Valores Extremos (Pickands-Balkema-de Haan
Sea \(X\) una variable aleatoria con distribución \(F\) y un nivel de umbral \(u\), entonces definimos:
\[F_{u}(y)=P(X-u\leq y |X>u)=\frac{F(y+u)-F(u)}{1-F(u)}\]
Entonces
\[\lim_{u\to\infty}F_{u}(y)=G(y)\]
Con $G(y) una distribución de Pareto Generalizada.
El segundo Teorema fundamental, nos indica que los excesos convegerán a una Distribución de Pareto Generalizada cuando el umbral \(u\) es suficientemente grande.
Definición
La función \(e(u)=E(X-u|X>u)\) se conoce como la función media de excesos.
Definición
Definimos la Distribución Generalizada de Pareto estándar (DGP) como:
\[ H_{\xi}(x)=\begin{cases} 1-(1+\xi x)^{-1/\xi} & \xi \neq 0 \\ 1-e^{-x} & \xi = 0 \end{cases} \] donde:
\[x \geq 0 \quad \text{si } \xi\geq0\]
\[-1/\xi \geq x \geq 0 \quad \text{si } \xi< 0\]
Al igual que el caso de las GEV podemos modificar su localización \(\mu\) y su forma \(\sigma\), tal que:
\[H_{\xi,u,\sigma}(x)=H_{\xi}((x-u)/\sigma)\]
** Tipos de distribución**
Al igual al caso de la GEV, podemos realizar tres tipos de parametrizaciones para las DGP:
Exponencial \(W_0=1-e^{-x}\) con \(x \geq 0\).
Pareto \(W_{1,\alpha}=1-x^{-\alpha}\) con \(x \geq 1, \alpha \geq 0\).
Beta \(W_{2,\alpha}=1-(-x)\alpha\) con \(0\geq x \geq -1, \alpha \geq 0\).
Ejemplo
Consideremos la base de datos, de los terremotos ocurridos en Fiji desde 1964 con una escala superior a 4.0, en total son 1 000
library(evd) #GEV
library(datasets)
summary(quakes) lat long depth mag
Min. :-38.59 Min. :165.7 Min. : 40.0 Min. :4.00
1st Qu.:-23.47 1st Qu.:179.6 1st Qu.: 99.0 1st Qu.:4.30
Median :-20.30 Median :181.4 Median :247.0 Median :4.60
Mean :-20.64 Mean :179.5 Mean :311.4 Mean :4.62
3rd Qu.:-17.64 3rd Qu.:183.2 3rd Qu.:543.0 3rd Qu.:4.90
Max. :-10.72 Max. :188.1 Max. :680.0 Max. :6.40
stations
Min. : 10.00
1st Qu.: 18.00
Median : 27.00
Mean : 33.42
3rd Qu.: 42.00
Max. :132.00 En este caso, no tenemos claridad cuando ocurrió cada temblor o si existieron periodos de muchos temblores.
datos<-quakes$mag
barplot(datos)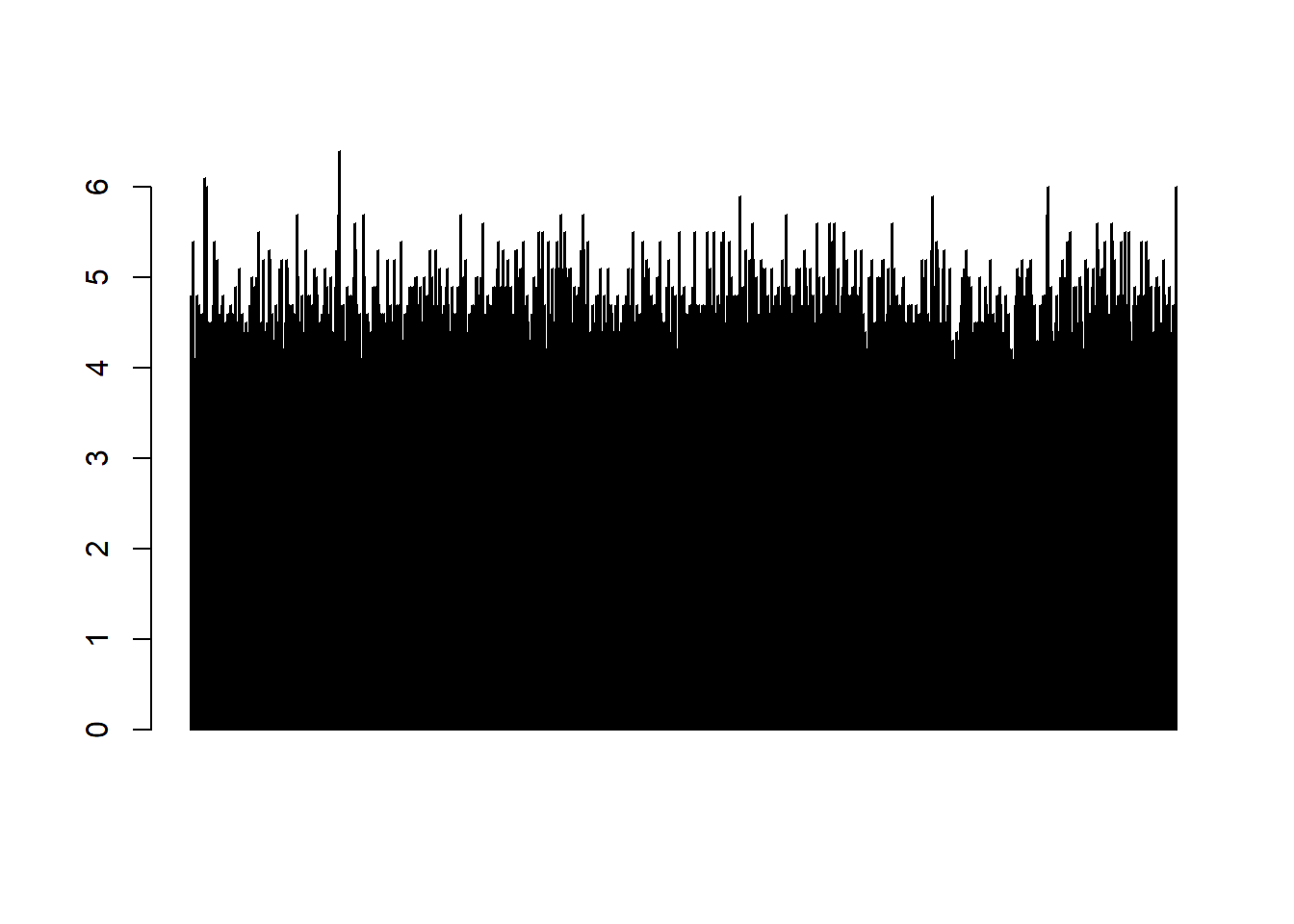
Usaremos del paquete evd la función fpot, eta función requiere que indiquemos el umbral (threshold)
fpot(datos,4)
Call: fpot(x = datos, threshold = 4)
Deviance: 909.3491
Threshold: 4
Number Above: 954
Proportion Above: 0.954
Estimates
scale shape
0.8329 -0.3411
Standard Errors
scale shape
0.02710 0.01237
Optimization Information
Convergence: successful
Function Evaluations: 58
Gradient Evaluations: 11 Para el caso de la Distribución de Pareto Generalizada, su esperanza esta dada por:
\[E[X]=u+\frac{\sigma}{1-\xi} \quad \text{si } \xi<1\] Para el ejemplo de los Temblores en Fiji, tenemos el siguiente valor:
4+(0.8329)/(1-(-0.3411))[1] 4.621057Si consideramos el ejemplo de la muestra normal, creando un umbral de 2, obtenemos el siguiente resultado
library(evd) #GEV
set.seed(2024)
BD=rnorm(10000,0,1)
fpot(BD,2)
Call: fpot(x = BD, threshold = 2)
Deviance: -6.727735
Threshold: 2
Number Above: 231
Proportion Above: 0.0231
Estimates
scale shape
0.4307 -0.1722
Standard Errors
scale shape
0.03851 0.06161
Optimization Information
Convergence: successful
Function Evaluations: 41
Gradient Evaluations: 9 Observe que en este caso, nos interesa todos los datos que superen el umbral, no importa en que bloque se encuentra el dato, por lo que no dividimos la muestra en bloques de 100.
cat("Esperanza Máxima Esperada")Esperanza Máxima Esperada2+(0.4307)/(1-(-0.1722))[1] 2.367429Si cambiamos el umbral a 2.5, obtenemos el siguiente resultado
fpot(BD,2.5)
Call: fpot(x = BD, threshold = 2.5)
Deviance: -43.78716
Threshold: 2.5
Number Above: 71
Proportion Above: 0.0071
Estimates
scale shape
0.3046 -0.1194
Standard Errors
scale shape
0.05283 0.12730
Optimization Information
Convergence: successful
Function Evaluations: 18
Gradient Evaluations: 6 cat("Esperanza Máxima Esperada")Esperanza Máxima Esperada2+(0.3046)/(1-(-0.1194))[1] 2.27211Podemos resumir el valor máximo esperado para las muestras analizada de la distribución normal estándar.
| Método | Máximo Esperado |
|---|---|
| Estadística de Orden | 2.330079 |
| GEV | 2.513518 |
| DPG u=2 | 2.367429 |
| DPG u=2.5 | 2.27211 |
Nota
En la práctica, el establecer el umbral \(u\) es importante, si es muy alto podemos tener pocas observaciones, o si es muy bajo podemos tener muchas observaciones que afecten el resultado.
Veamos los resultado con la distribución exponencial con esperanza igual a 10, para esto usaremos tres umbrales de 30, 40 y 35, y vemos el cambio en la esperanza máxima esperada de la atención.
library(evd) #GEV
set.seed(2024)
BD=rexp(10000,1/10)
fpot(BD,30)
Call: fpot(x = BD, threshold = 30)
Deviance: 3115.067
Threshold: 30
Number Above: 469
Proportion Above: 0.0469
Estimates
scale shape
10.119494 0.006503
Standard Errors
scale shape
0.71481 0.05345
Optimization Information
Convergence: successful
Function Evaluations: 16
Gradient Evaluations: 4 cat("Esperanza Máxima Esperada")Esperanza Máxima Esperada30+(10.119494)/(1-(0.006503))[1] 40.18573fpot(BD,40)
Call: fpot(x = BD, threshold = 40)
Deviance: 1127.559
Threshold: 40
Number Above: 166
Proportion Above: 0.0166
Estimates
scale shape
13.1465 -0.1799
Standard Errors
scale shape
1.48538 0.08328
Optimization Information
Convergence: successful
Function Evaluations: 29
Gradient Evaluations: 7 cat("Esperanza Máxima Esperada")Esperanza Máxima Esperada40+(13.1465)/(1-(-0.1799))[1] 51.14205fpot(BD,45)
Call: fpot(x = BD, threshold = 45)
Deviance: 719.9928
Threshold: 45
Number Above: 107
Proportion Above: 0.0107
Estimates
scale shape
13.7260 -0.2549
Standard Errors
scale shape
1.8825 0.1004
Optimization Information
Convergence: successful
Function Evaluations: 29
Gradient Evaluations: 8 cat("Esperanza Máxima Esperada")Esperanza Máxima Esperada45+(13.7260)/(1-(-0.2549))[1] 55.93792| Método | Máximo Esperado |
|---|---|
| Estadística de Orden | 46.15121 |
| GEV | 50.57038 |
| DPG u=30 | 40.18573 |
| DPG u=40 | 51.14205 |
| DPG u=45 | 55.93792 |